10．如图9－2－24所示，足够长的光滑平行金属导轨MN、PQ竖直放置，一个磁感应强度B＝0.50 T的匀强磁场垂直穿过导轨平面，导轨的上端M与P间连接阻值为R＝0.30 Ω的电阻，长为L＝0.40 m、电阻为r＝0.20 Ω的金属棒ab紧贴在导轨上．现使金属棒ab由静止开始下滑，通过传感器记录金属棒ab下滑的距离，其下滑距离与时间的关系如下表所示，导轨电阻不计．(g＝10 m/s²)求：

(1)在前0.4 s的时间内，金属棒ab电动势的平均值；,

(2)金属棒的质量；,

(3)在前0.7 s的时间内，电阻R上产生的热量.

解析：(1)＝＝＝0.6 V.

(2)从表格中数据可知，0.3 s后棒做匀速运动，速度v＝＝5 m/s

由mg－F＝0，F＝BIL，I＝，E＝BLv，解得m＝0.04 kg.

(3)棒在下滑过程中，有重力和安培力做功，克服安培力做的功等于回路的焦耳热．则：

mgs－Q＝mv²－0，Q_R＝Q，解得Q＝0.348 J.

答案：(1)0.6 V　(2)0.04 kg　(3)0.348 J

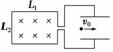
图9－2－25

9．如图9－2－23所示，一无限长的光滑金属平行导轨置于匀强磁场B中，磁场方向垂直导轨平面，导轨平面竖直且与地面绝缘，导轨上M、N间接一电阻R，P、Q端接一对沿水平方向的平行金属板，导体棒ab置于导轨上，其电阻为3R，导轨电阻不计，棒长为L，平行金属板间距为d.今导体棒通过定滑轮在一物块拉动下开始运动，稳定后棒的速度为v，不计一切摩擦阻力．此时有一带电量为q的液滴恰能在两板间做半径为r的匀速圆周运动，且速率也为v.求：

(1)棒向右运动的速度v；

(2)物块的质量m.

解析：(1)设带电液滴的质量为m₀，对于液滴：qvB＝m₀，m₀g＝q

对导体棒匀速运动时：E＝BLv，I＝，U＝IR

由以上各式联立解得：v＝2 .

(2)对导体棒ab水平方向：mg＝BIL，由以上各式联立可得：m＝.

答案：(1)2 　(2)

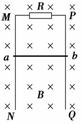
图9－2－24

8．(2009·郑州调研)如图9－2－22(甲)所示，面积S＝0.2 m²的线圈，匝数n＝630匝，总电阻r＝1.0 Ω，线圈处在变化的磁场中，设磁场垂直纸面向外为正方向，磁感应强度B随时间t按图(乙)所示规律变化，方向垂直线圈平面，图(甲)中传感器可看成一个纯电阻R，并标有“3 V、0.9 W”，滑动变阻器R₀上标有“10 Ω，1 A”，则下列说法正确的是(　)

A．电流表的电流方向向左

B．为了保证电路的安全，电路中允许通过的最大电流为1 A

C．线圈中产生的感应电动势随时间在变化

D．若滑动变阻器的滑片置于最左端，为了保证电路的安全，图9－2－23(乙)中的t₀最小值为40 s

解析：由楞次定律可知：电流表的电流方向向右；又传感器正常工作时的电阻R＝＝＝10 Ω，工作电流I＝＝＝0.3 A，由于滑动变阻器工作电流是1 A，所以电路允许通过的最大电流为I_max＝0.3 A；由于磁场时间均匀变化，所以线圈中产生的感应电动势是不变的．滑动变阻器的滑片位于最左端时外电路的电阻为R_外＝20 Ω，故电流电动势的最大值E＝＝＝，解得t₀＝40 s．故只有D项正确．

答案：D

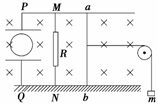
图9－2－23

7．如图9－2－21所示在虚线空间内有一对彼此平行的金属导轨，宽为L，与水平面的夹角为θ，导轨电阻不计，在虚线空间内同时分布着垂直导轨平面向上的磁感应强度为B的匀强磁场．导轨的下端接一定值电阻R，上端通过导线与一对竖直放置的平行金属板相连接，两板间距为d，其间固定着一光滑绝缘直杆，它与水平面也成θ角，杆上套一带电小球．当一电阻也为R的光滑导体棒ab沿导轨以速度v匀速下滑时，小球恰好静止在绝缘直杆上．则由此可以判断小球的电性并能求出其荷质比为(　)

A．正电荷，2dgtan θ/BLvcos θ　　 B．正电荷，2dgtan θ/BLv

C．负电荷，2dgtan θ/BLvcos θ　　 D．负电荷，2dgtan θ/BLv

解析：杆切割磁感线产生的感应电动势为BLv，所以U＝BLv/2，对球：qU/d＝mgtan θ，联立得q/m＝2dgtan θ/BLv，故正确答案为B.

答案：B

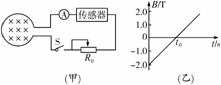
图9－2－22

6．如图9－2－20甲所示，固定在水平桌面上的光滑金属框架cdeg处于方向竖直向下的匀强磁场中，金属杆ab与金属框架接触良好．在两根导轨的端点d、e之间连接一电阻R，其他部分电阻忽略不计．现用一水平向右的外力F作用在金属杆ab上，使金属杆由静止开始向右在框架上滑动，运动中杆ab始终垂直于框架．图乙为一段时间内金属杆中的电流I随时间t的变化关系图象，则下列选项中可以表示外力F随时间t变化关系的图象是(　)

解析：金属杆由静止开始向右在框架上滑动，金属杆切割磁感线产生感应电动势E＝BLv，在回路内产生感应电流I＝E/R＝BLv/R.由题图乙金属杆中的电流I随时间t均匀增大可知金属杆做初速度为零的匀加速运动，I＝BLat/R.由安培力公式可知金属杆所受安培力F_安＝BIL，根据牛顿第二定律F－F_安＝ma可得外力F＝ma+BIL＝ma+B²L²at/R，所以正确选项是B.

答案：B

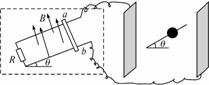
图9－2－21

5．在匀强磁场中，有一个接有电容器的单匝导线回路，如图9－2－19所示，已知C＝30 μF，L₁＝5 cm，L₂＝8 cm，磁场以5×10^－2 T/s的速率增加，则(　)

A．电容器上极板带正电，带电荷量为6×10^－5 C

B．电容器上极板带负电，带电荷量为6×10^－5 C

C．电容器上极板带正电，带电荷量为6×10^－9 C

D．电容器上极板带负电，带电荷量为6×10^－9 C

解析：电容器两极板间的电势差U等于感应电动势E，由法拉第电磁感应定律，可得E＝·L₁L₂＝2×10^－4 V，电容器的带电荷量Q＝CU＝CE＝6×10^－9 C，再由楞次定律可知上极板的电势高，带正电，C项正确．

答案：C

图9－2－20

4.

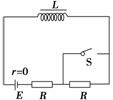
图9－2－18

如图9－2－18所示，多匝电感线圈L的电阻不计，两个电阻的阻值都是R，电键S原来打开，通过电源的电流I₀＝，合上电键，线圈中有自感电动势，这个电动势将(　)

A．有阻碍电流的作用，最后电流由I₀减小到零

B．有阻碍电流的作用，最后电流小于I₀

C．有阻碍电流增大的作用，因而电流I₀保持不变

D．有阻碍电流增大的作用，但最后电流还是增大到2I₀

答案：D

图9－2－19

3．(2009·山东，2)如图9－2－17所示，一导线弯成半径为a的半圆形闭合回路．虚线MN右侧有磁感应强度为B的匀强磁场，方向垂直于回路所在的平面．回路以速度v向右匀速进入磁场，直径CD始终与MN垂直．从D点到达边界开始到C点进入磁场为止，下列结论正确的是(　)

A．感应电流方向不变　　　　　　　 B．CD段直导线始终不受安培力

C．感应电动势最大值E_m＝Bav　　　 D．感应电动势平均值＝πBav

解析：根据楞次定律可判定闭合回路中产生的感应电流方向始终不变，A项正确；CD段电流方向是D指向C，根据左手定则可知，CD段受到安培力，且方向竖直向下，B项错；当有一半进入磁场时，产生的感应电流最大，E_m＝Bav，C项对；由法拉第电磁感应定律得＝＝，D项也对．

答案：ACD

2．如图9－2－16中半径为r的金属圆盘在垂直于盘面的匀强磁场B中，绕O轴以角速度ω沿逆时针方向匀速转动，则通过电阻R的电流的大小和方向是(金属圆盘的电阻不计)(　)

A．由c到d，I＝Br²ω/R　　　 B．由d到c，I＝Br²ω/R

C．由c到d，I＝Br²ω/(2R)　　 D．由d到c，I＝Br²ω/(2R)

解析：金属圆盘在匀强磁场中匀速转动，可以等效为无数根长为r的导体棒绕O点做匀速圆周运动，其产生的感应电动势大小为E＝Br²ω/2，由右手定则可知其方向由外指向圆心，故通过电阻R的电流I＝Br²ω/(2R)，方向由d到c，故选D项．

答案：D

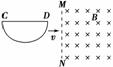
图9－2－17

1．下列关于感应电动势大小的说法中，正确的是(　)

A．线圈中磁通量变化越大，线圈中产生的感应电动势一定越大

B．线圈中磁通量越大，产生的感应电动势一定越大

C．线圈放在磁感应强度越强的地方，产生的感应电动势一定越大

D．线圈中磁通量变化越快，产生的感应电动势越大

解析：由法拉第电磁感应定律E＝n知，感应电动势与磁通量的变化率成正比，与磁通量的大小、磁通量的变化和磁感应强度无关，故只有D项正确．

答案：D

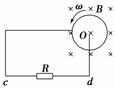
图9－2－16