
第一节(共5小题,每题1.5分,满分7.5分)
听下面5段对话,回答1至5小题。
1. What time will the woman meet the man?
A. At 10:00. B. At 10:20. C. At 10:40.
2. When do the speakers plan to have a picnic?
A. In the early morning. B. In the mid-morning. C. In the afternoon.
3. Where does this conversation most probably take place?
A. At a clothing store. B. At a tailor’s shop. C. At a sports center.
4. What are the speakers talking about?
A. Patience. B. Interests. C. Challenges.
5. What are the two speakers going to do?
A. Try to phone Ann. B. Go to look for Ann. C. Wait for Ann till 11:00.
23、(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
已知数列 满足:
满足: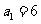 ,
,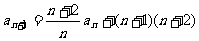 。
。
(1)若 ,求数列
,求数列 的通项公式;
的通项公式;
(2) 若 ,(其中
,(其中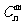 表示组合数),求数列
表示组合数),求数列 的前
的前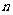 项和
项和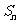 ;
;
(3)若 ,记数列
,记数列 的前
的前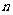 项和为
项和为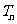 ,求
,求 ;
;
22. (本题满分16分,第(1)小题4分,第(2)小题6分,第(3)小题6分)
已知椭圆C的长轴长与短轴长之比为 ,焦点坐标分别为
,焦点坐标分别为 ,
,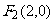 。
。
(1)求椭圆C的标准方程;
(2)已知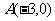 ,
,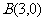 ,
,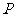 是椭圆C上异于
是椭圆C上异于 、
、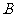 的任意一点,直线
的任意一点,直线 、
、 分别交y轴于
分别交y轴于 、
、 ,求
,求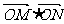 的值;
的值;
(3)在(2)的条件下,若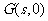 ,
,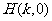 ,且
,且 ,
,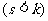 ,分别以OG、OH为边作两正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标
,分别以OG、OH为边作两正方形,求此两正方形的面积和的最小值,并求出取得最小值时的G、H点坐标
21、 (本题满分14分,第(1)小题6分,第(2)小题8分)
(1)已知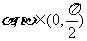 ,且
,且 ,比较
,比较 与
与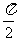 的大小;
的大小;
(2)试确定一个区间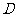 ,
, ,对任意的
,对任意的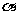 、
、 ,当
,当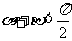 时,恒有
时,恒有 ;并说明理由。
;并说明理由。
说明:对于第(2)题,将根据写出区间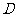 所体现的思维层次和对问题探究的完整性,给予不同的评分.
所体现的思维层次和对问题探究的完整性,给予不同的评分.
20、(本题满分14分,第(1)小题6分,第(2)小题8分)
已知函数 ;
;
(1)证明:函数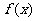 在
在 上为减函数;
上为减函数;
(2)是否存在负数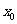 ,使得
,使得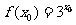 成立,若存在求出
成立,若存在求出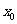 ;若不存在,请说明理由。
;若不存在,请说明理由。
19、 (本题满分12分)
(本题满分12分)
如图,已知三棱柱 是直三棱柱,
是直三棱柱,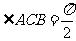 ,若用此直三棱柱作为无盖盛水容器,容积为
,若用此直三棱柱作为无盖盛水容器,容积为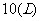 ,高为
,高为 ,盛水时发现在D、E两处有泄露,且D、E分别在棱
,盛水时发现在D、E两处有泄露,且D、E分别在棱 和
和 上,
上, 
 ,
, 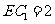
 。试问现在此容器最多能盛水多少(
。试问现在此容器最多能盛水多少(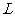 )?
)?
18、已知圆 与
与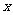 轴的两个交点为
轴的两个交点为 、
、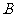 ,若圆内的动点
,若圆内的动点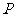 使
使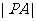 、
、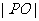 、
、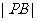 成等比数列,则
成等比数列,则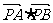 的取值范围为--------------( )
的取值范围为--------------( )
(A)  (B)
(B) (C)
(C) (D)
(D)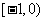
17、若 存在,则实数
存在,则实数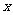 的取值范围为-------( )
的取值范围为-------( )
(A)  (B)
(B)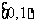 (C)
(C)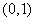 (D)
(D)
16、下列4个命题中:
(1)存在 使不等式
使不等式
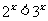 成立
成立
(2)不存在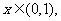 使不等式
使不等式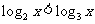 成立
成立
(3)任意的 使不等式
使不等式 成立
成立
(4)任意的 使不等式
使不等式 成立
成立
真命题的是 ---------------( )
(A) (1)、(3) (B) (1)、(4) (C) (2)、(3) (D) (2)、(4)
15、已知一球半径为2,球面上A、B两点的球面距离为 ,则线段AB的长度为( )
,则线段AB的长度为( )
(A) 1 (B) (C)
2 (D) 2
(C)
2 (D) 2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com