
2.下列词语中,没有错别字的一项是( )
A.妙手偶得 举指泰然 顶礼膜拜
B.孤陋寡闻 声嘶力竭 神彩奕奕
C.大名鼎鼎 温文而雅 未雨绸谬
D.煞有介事 黯然失色 手舞足蹈
1.下列对加点字的注音,有错的一项是( )
A.淅沥(xī) 喇叭声咽(yè) B.阔绰(chuò) 五行缺土(xín)
C.休憩(qì) 惴惴不安(zhuì) D.阴霾(mái) 涸泽的鱼(hé)
本卷包括必考题和选考题两部分,第(13)题~第(21)题为必考题,每个试题考生都必须做答,第(22)题~第(24)题为选考题,考试根据要求做答。
(13)设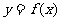 为区间
为区间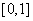 上的连续函数,且恒有
上的连续函数,且恒有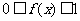 ,可以用随机模拟方法近似计算积分
,可以用随机模拟方法近似计算积分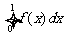 ,先产生两组(每组N个)区间
,先产生两组(每组N个)区间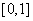 上的均匀随机数
上的均匀随机数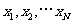 和
和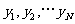 ,由此得到N个点
,由此得到N个点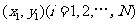 ,再数出其中满足
,再数出其中满足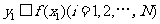 的点数
的点数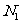 ,那么由随机模拟方案可得积分
,那么由随机模拟方案可得积分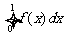 的近似值为 。
的近似值为 。
[答案]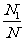
解析: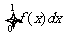 的几何意义是函数
的几何意义是函数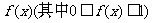 的图像与
的图像与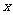 轴、直线
轴、直线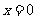 和直线
和直线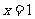 所围成图形的面积,根据几何概型易知
所围成图形的面积,根据几何概型易知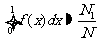 .
.
(14)正视图为一个三角形的几何体可以是______(写出三种)
[解析]三棱锥、三棱柱、圆锥等.
(15)过点A(4,1)的圆C与直线x-y=0相切于点B(2,1),则圆C的方程为____
[答案]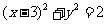
解析:设圆的方程为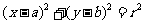 ,则根据已知条件得
,则根据已知条件得
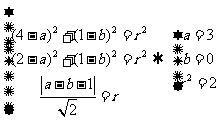 .
.
(16)在△ABC中,D为边BC上一点,BD=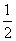 DC,
DC, ADB=120°,AD=2,若△ADC的面积为
ADB=120°,AD=2,若△ADC的面积为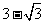 ,则
,则 BAC=_______
BAC=_______
[答案]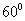
解析:设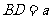 ,则
,则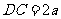 ,由已知条件有
,由已知条件有
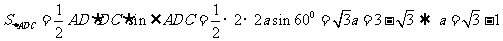 ,再由余弦定理分别得到
,再由余弦定理分别得到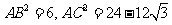 ,再由余弦定理得
,再由余弦定理得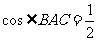 ,所以
,所以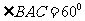 .
.
三,解答题:解答应写出文字说明,正明过程和演算步骤
(17)(本小题满分12分)
设数列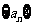 满足
满足
(1)
求数列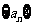 的通项公式;
的通项公式;
(2)
令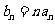 ,求数列的前n项和
,求数列的前n项和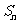
(17)解:
(Ⅰ)由已知,当n≥1时,
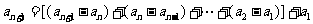
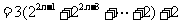
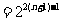 。
。
而 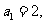
所以数列{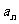 }的通项公式为
}的通项公式为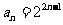 。
。
(Ⅱ)由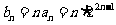 知
知
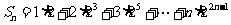 ①
①
从而
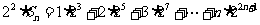 ②
②
①-②得
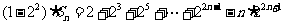 。
。
 即
即 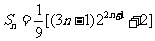
(18)(本小题满分12分)
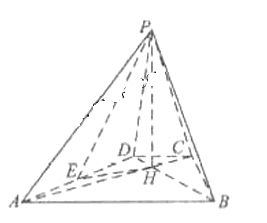
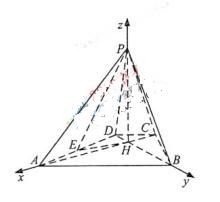
如图,已知四棱锥P-ABCD的底面为等腰梯形,AB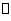 CD,AC
CD,AC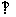 BD,垂足为H,PH是四棱锥的高 ,E为AD中点
BD,垂足为H,PH是四棱锥的高 ,E为AD中点
(1)
证明:PE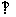 BC
BC
(2)
若 APB=
APB= ADB=60°,求直线PA与平面PEH所成角的正弦值
ADB=60°,求直线PA与平面PEH所成角的正弦值
(18)解:
以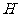 为原点,
为原点,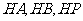 分别为
分别为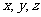 轴,线段
轴,线段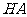 的长为单位长, 建立空间直角坐标系如图, 则
的长为单位长, 建立空间直角坐标系如图, 则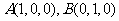
(Ⅰ)设 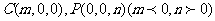
则 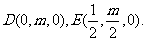
可得 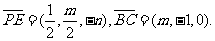
因为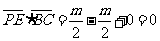
所以 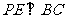
(Ⅱ)由已知条件可得
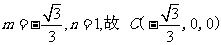
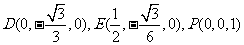
设 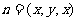 为平面
为平面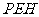 的法向量
的法向量
则 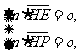 即
即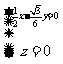
因此可以取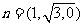 ,
,
由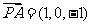 ,
,
可得 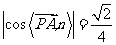
所以直线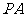 与平面
与平面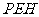 所成角的正弦值为
所成角的正弦值为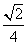
(19)(本小题12分)
为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
|
是否需要志愿 性别 |
男 |
女 |
|
需要 |
40 |
30 |
|
不需要 |
160 |
270 |
(1) 估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2) 能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3) 根据(2)的结论,能否提供更好的调查方法来估计该地区老年人,需要志愿帮助的老年人的比例?说明理由
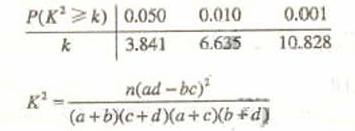 附:
附:
(19)解:
(1)调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例的估算值为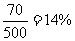
(2)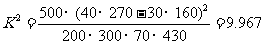 。
。
由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关。
(III)由(II)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据能看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异,因此在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层并采用分层抽样方法比采用简单随机抽样方法更好.
(20)(本小题满分12分)
设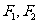 分别是椭圆
分别是椭圆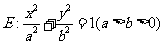 的左、右焦点,过
的左、右焦点,过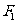 斜率为1的直线
斜率为1的直线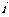 与
与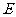 相交于
相交于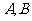 两点,且
两点,且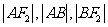 成等差数列。
成等差数列。
(1)求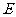 的离心率;
的离心率;
(2) 设点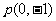 满足
满足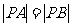 ,求
,求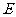 的方程
的方程
20.)解:
(I)由椭圆定义知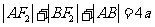 ,又
,又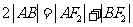 ,
,
得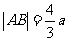
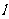 的方程为
的方程为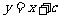 ,其中
,其中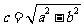 。
。
设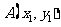 ,
,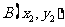 ,则A、B两点坐标满足方程组
,则A、B两点坐标满足方程组
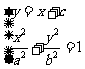
化简的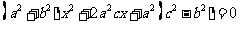
则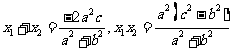
因为直线AB斜率为1,所以

得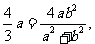 故
故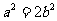
所以E的离心率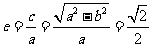
(II)设AB的中点为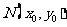 ,由(I)知
,由(I)知
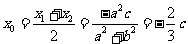 ,
,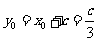 。
。
由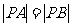 ,得
,得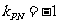 ,
,
即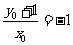
得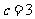 ,从而
,从而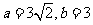
故椭圆E的方程为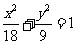 。
。
(21)(本小题满分12分)
设函数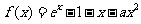 。
。
(1)
若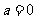 ,求
,求 的单调区间;
的单调区间;
(2) 若当 时
时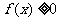 ,求
,求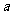 的取值范围
的取值范围
(21)解:
(1)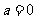 时,
时,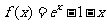 ,
,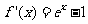 .
.
当 时,
时,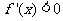 ;当
;当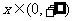 时,
时,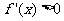 .故
.故 在
在 单调减少,在
单调减少,在 单调增加
单调增加
(II)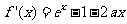
由(I)知 ,当且仅当
,当且仅当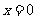 时等号成立.故
时等号成立.故
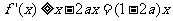 ,
,
从而当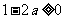 ,即
,即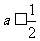 时,
时,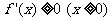 ,而
,而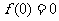 ,
,
于是当 时,
时,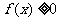 .
.
由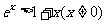 可得
可得 .从而当
.从而当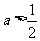 时,
时,
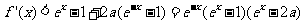 ,
,
故当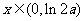 时,
时,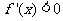 ,而
,而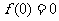 ,于是当
,于是当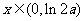 时,
时,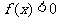 .
.
综合得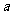 的取值范围为
的取值范围为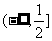 .
.
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。
(22)(本小题满分10分)选修4-1:几何证明选讲
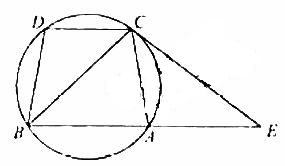
如图,已经圆上的弧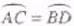 ,过C点的圆切线与BA的延长线交于E点,证明:
,过C点的圆切线与BA的延长线交于E点,证明:
(Ⅰ)∠ACE=∠BCD;
(Ⅱ)BC2=BF×CD。
(22)解:
(I)因为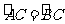 ,
,
所以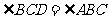 .
.
又因为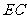 与圆相切于点
与圆相切于点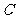 ,故
,故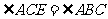 ,
,
所以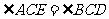 .
.
(II)因为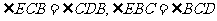 ,
,
所以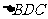 ∽
∽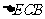 ,故
,故 ,
,
即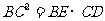 .
.
(23)(本小题满分10分)选修4-4:坐标系与参数方程
已知直线C1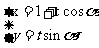 (t为参数),C2
(t为参数),C2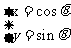 (
(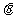 为参数),
为参数),
(Ⅰ)当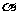 =
=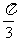 时,求C1与C2的交点坐标;
时,求C1与C2的交点坐标;
(Ⅱ)过坐标原点O做C1的垂线,垂足为 ,P为OA中点,当
,P为OA中点,当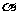 变化时,求P点的轨迹的参数方程,并指出它是什么曲线。
变化时,求P点的轨迹的参数方程,并指出它是什么曲线。
(23)解:
(Ⅰ)当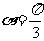 时,
时,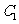 的普通方程为
的普通方程为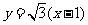 ,
,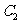 的普通方程为
的普通方程为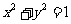 。联立方程组
。联立方程组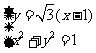 ,解得
,解得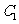 与
与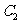 的交点为(1,0)
的交点为(1,0)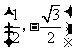 。
。
(Ⅱ)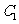 的普通方程为
的普通方程为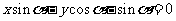 。
。
A点坐标为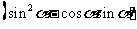 ,
,
故当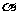 变化时,P点轨迹的参数方程为:
变化时,P点轨迹的参数方程为:

P点轨迹的普通方程为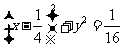 。
。
故P点轨迹是圆心为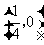 ,半径为
,半径为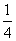 的圆。
的圆。
(24)(本小题满分10分)选修4-5,不等式选项
设函数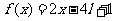
(Ⅰ)画出函数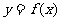 的图像
的图像
(Ⅱ)若不等式 ≤
≤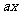 的解集非空,求a的取值范围。
的解集非空,求a的取值范围。
(24) 解:
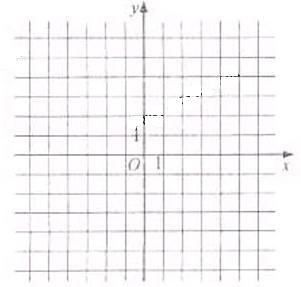
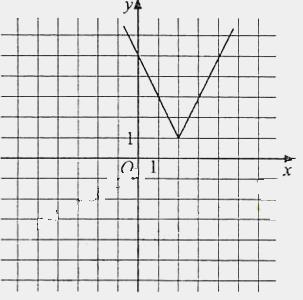 (Ⅰ)由于
(Ⅰ)由于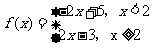 则函数
则函数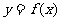 的图像如图所示。
的图像如图所示。
(Ⅱ)由函数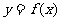 与函数
与函数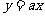 的图像可知,当且仅当
的图像可知,当且仅当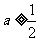 或
或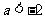 时,函数
时,函数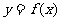 与函数
与函数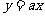 的图像有交点。故不等式
的图像有交点。故不等式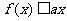 的解集非空时,
的解集非空时,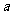 的取值范围为
的取值范围为
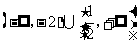 。
。
1.已知集合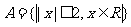 },
},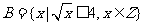 ,则
,则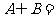
(A)(0,2) (B)[0,2] (C){0,2] (D){0,1,2}
[答案]D
解析:由已知得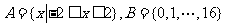 ,所以
,所以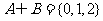 .
.
(2)已知复数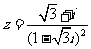 ,
,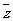 是z的共轭复数,则
是z的共轭复数,则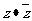 =
=
A. 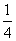 B.
B.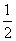 C.1
D.2
C.1
D.2
[答案]A
解析: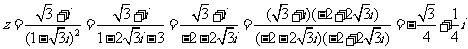 ,
,
所以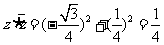 .
.
另解: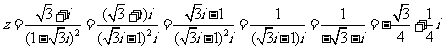 ,下略.
,下略.
(3)曲线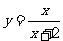 在点(-1,-1)处的切线方程为
在点(-1,-1)处的切线方程为
(A)y=2x+1 (B)y=2x-1 C y=-2x-3 D.y=-2x-2
[答案]A
解析: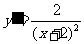 ,所以
,所以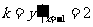 ,故切线方程为
,故切线方程为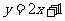 .
.
另解:将点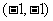 代入可排除B、D,而
代入可排除B、D,而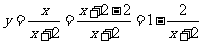 ,由反比例函数
,由反比例函数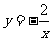 的图像,再根据图像平移得在点
的图像,再根据图像平移得在点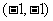 处的切线斜率为正,排除C,从而得A.
处的切线斜率为正,排除C,从而得A.
(4)如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(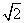 ,-
,-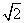 ),角速度为1,那么点P到x轴距离d关于时间t的函数图像大致为
),角速度为1,那么点P到x轴距离d关于时间t的函数图像大致为
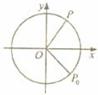
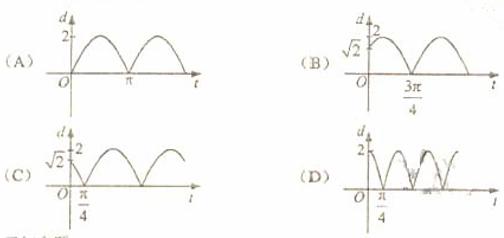
[答案]C
解析:显然,当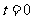 时,由已知得
时,由已知得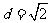 ,故排除A、D,又因为质点是按逆时针方向转动,随时间
,故排除A、D,又因为质点是按逆时针方向转动,随时间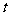 的变化质点P到
的变化质点P到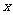 轴的距离
轴的距离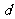 先减小,再排除B,即得C.
先减小,再排除B,即得C.
另解:根据已知条件得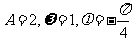 ,再结合已知得质点P到
,再结合已知得质点P到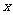 轴的距离
轴的距离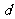 关于时间
关于时间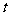 的函数为
的函数为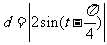 ,画图得C.
,画图得C.
(5)已知命题
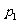 :函数
:函数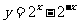 在R为增函数,
在R为增函数,
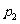 :函数
:函数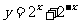 在R为减函数,
在R为减函数,
则在命题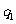 :
: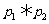 ,
,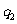 :
: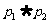 ,
,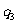 :
: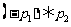 和
和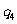 :
: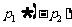 中,真命题是
中,真命题是
(A)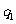 ,
,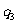 (B)
(B)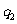 ,
,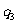 (C)
(C)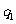 ,
,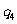 (D)
(D)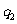 ,
,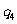
[答案]C
解析:易知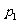 是真命题,而对
是真命题,而对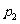 :
: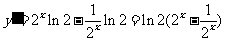 ,当
,当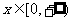 时,
时,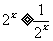 ,又
,又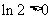 ,所以
,所以 ,函数单调递增;同理得当
,函数单调递增;同理得当 时,函数单调递减,故
时,函数单调递减,故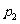 是假命题.由此可知,
是假命题.由此可知,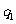 真,
真,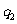 假,
假,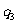 假,
假,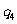 真.
真.
另解:对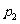 的真假可以取特殊值来判断,如取
的真假可以取特殊值来判断,如取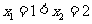 ,得
,得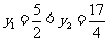 ;取
;取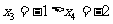 ,得
,得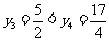 即可得到
即可得到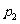 是假命题,下略.
是假命题,下略.
(6)某种种子每粒发芽的概率都为0.9,现播种了1000粒,对于没有发芽的种子,每粒需再补种2粒,补种的种子数记为X,则X的数学期望为
(A)100 (B)200 (C)300 (D)400
[答案]B
解析:根据题意显然有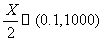 ,所以
,所以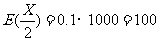 ,故
,故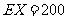 .
.
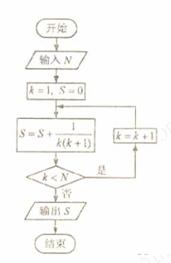
(7)如果执行右面的框图,输入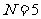 ,则输出的数等于
,则输出的数等于
(A)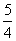
(B)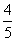
(C)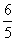
(D)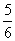
[答案]D
解析:根据题意满足条件的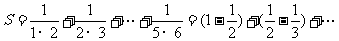
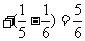 .
.
(8)设偶函数 满足
满足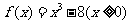 ,则
,则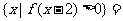
(A) 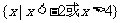 (B)
(B)
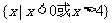
(C) 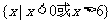 (D)
(D) 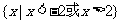
[答案]B
解析:当 时,
时,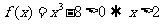 ,又由于函数是偶函数,所以
,又由于函数是偶函数,所以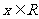 时,
时,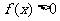 的解集为
的解集为 或
或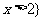 ,故
,故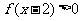 的解集为
的解集为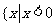 或
或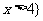 .
.
另解:根据已知条件和幂函数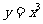 的图像易知
的图像易知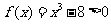 的解集为
的解集为 或
或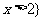 ,故
,故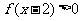 的解集为
的解集为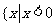 或
或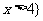 .
.
(9)若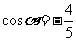 ,
,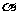 是第三象限的角,则
是第三象限的角,则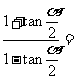
(A) 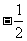 (B)
(B)
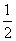 (C) 2 (D) -2
(C) 2 (D) -2
[答案]A
解析:由已知得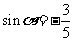 ,所以
,所以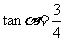 ,又
,又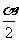 属于第二或第四象限,故由
属于第二或第四象限,故由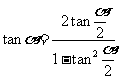 解得:
解得: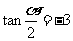 ,从而
,从而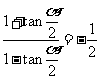 .
.
另解:由已知得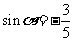 ,所以
,所以
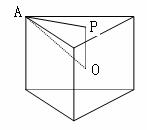
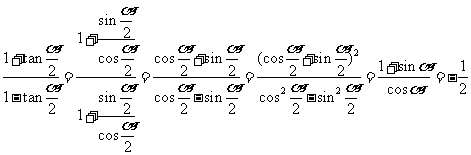 .
.
(10)设三棱柱的侧棱垂直于底面,所有棱长都为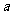 ,顶点都在一个球面上,则该球的表面积为
,顶点都在一个球面上,则该球的表面积为
(A) 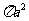 (B)
(B) 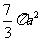 (C)
(C) 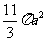 (D)
(D) 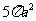
[答案]B
解析:如图,P为三棱柱底面中心,O为球心,易知
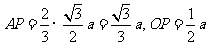 ,所以球的半径
,所以球的半径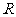 满足:
满足:
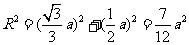 ,故
,故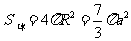 .
.
(11)已知函数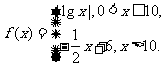 若
若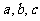 互不相等,且
互不相等,且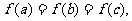 则
则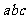 的取值范围是
的取值范围是
(A) 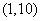 (B)
(B) 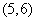 (C)
(C) 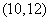 (D)
(D)
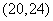
[答案]C
解析:不妨设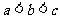 ,取特例,如取
,取特例,如取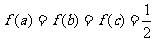 ,则易得
,则易得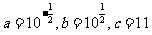 ,从而
,从而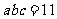 ,选C.
,选C.
另解:不妨设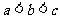 ,则由
,则由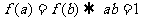 ,再根据图像易得
,再根据图像易得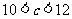 ,故选C.
,故选C.
(12)已知双曲线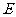 的中心为原点,
的中心为原点,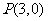 是
是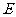 的焦点,过F的直线
的焦点,过F的直线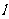 与
与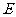 相交于A,B两点,且AB的中点为
相交于A,B两点,且AB的中点为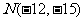 ,则
,则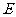 的方程式为
的方程式为
(A) 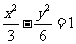 (B)
(B) 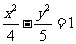 (C)
(C) 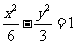 (D)
(D)
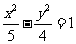
[答案]B
解析:由已知条件易得直线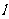 的斜率为
的斜率为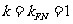 ,设双曲线方程为
,设双曲线方程为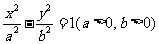 ,
,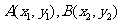 ,则有
,则有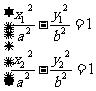 ,两式相减并结合
,两式相减并结合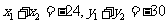 得,
得,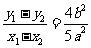 ,从而
,从而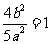 ,即
,即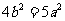 ,又
,又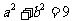 ,解得
,解得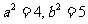 ,故选B.
,故选B.
第Ⅱ卷
4.

图3-3-12
如图3-3-12所示,在光滑的水平面上放着紧靠在一起的A、B两物体,B的质量是A的2倍,B受到向右的恒力FB=2 N,A受到的水平力FA=(9-2t) N(t的单位是s).从t=0开始计时,则( )
A.A物体在3 s末时刻的加速度是初始时刻的倍
B.t>4 s后,B物体做匀加速直线运动
C.t=4.5 s时,A物体的速度为零
D.t>4.5 s后,A、B的加速度方向相反
解析:对于A、B整体根据牛顿第二定律有FA+FB=(mA+mB)a,开始时合力为11 N,3秒末合力为5 N,故A正确.设A、B间的作用力为FN,则对B进行分析,由牛顿第二定律可得:FN+FB=mBa,解得FN=mB-FB= N.当t=4 s时,FN=0,A、B两物体开始分离,此后B做匀加速直线运动,故B正确;而A做加速度逐渐减小的加速运动,当t=4.5 s时,A物体的加速度为零而速度不为零,故C错误.t>4.5 s后,A所受合外力反向,即A、B的加速度方向相反,故D正确.当t<4 s时,A、B的加速度均为a=.综上所述,选项A、B、D正确.
答案:ABD
3.如右图所示,车厢里悬挂着两个质量不同的小球,上面的球比下面的球质量大,当车厢向右做匀加速运动时(空气阻力不计),两个小球稳定后所处的位置下列各图中正确的是( )
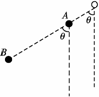

解析:两个小球稳定后与车厢一起向右做匀加速运动,它们的加速度
相同,先使用整体法求得a=gtan θ,再使用隔离法研究B物体a=
gtan θ,与竖直方向的角度相同,所以OA与AB在一条线上,B正
确.
答案:B
2.
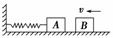
图3-3-11
如图3-3-11所示,在光滑的水平面上,A、B两物体的质量mA=2mB,A物体与轻质弹簧相连,弹簧的另一端固定在竖直墙上,开始时,弹簧处于自由状态,当物体B沿水平向左运动,使弹簧压缩到最短时,A、B两物体间作用力为F,则弹簧给A物体的作用力的大小为( )
A.F B.2F C.3F D.4F
解析:对B由牛顿第二定律得F=mBa①
对A、B整体由牛顿第二定律得F弹=(mA+mB)a②
mA=2mB③
由①②③得:F弹=3F,所以选项C正确.
答案:C
1.
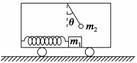
图3-3-10
(2010·日照模拟)在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根轻质弹簧相连接,弹簧的劲度系数为k.在车厢的顶部用一根细线悬挂一质量为m2的小球.某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢保持相对静止,如图3-3-10所示.不计木块与车厢底部的摩擦力,则在这段时间内弹簧的形变为( )
A.伸长量为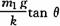 B.压缩量为
B.压缩量为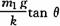
C.伸长量为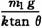 D.压缩量为
D.压缩量为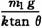
解析:分析m2的受力情况可得:m2gtan θ=m2a,得出:a=gtan θ,再对m1应用牛顿第二定律,得:kx=m1a,x=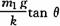 ,因a的方向向左,故弹簧处于伸长状态,故A正确.
,因a的方向向左,故弹簧处于伸长状态,故A正确.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com