
19. [解析]解法一:(Ⅰ)在直三棱柱ABC-A1B1C1中,∵CC1⊥
[解析]解法一:(Ⅰ)在直三棱柱ABC-A1B1C1中,∵CC1⊥
平面ABC,∴CC1⊥AC,∵BC=CC1,∴BCC1B1为正方形.∴BC1
⊥B1C(2分),又∵∠ACB=90°,∴AC⊥BC∴AC⊥平面BCC1B1,
∵B1C为AB1在平面BCC1B1内的射影,BC1⊥B1C,∴AB1⊥BC1,
(4分)
(Ⅱ)∵BC//B1C,∴BC//平面AB1C1,∴点B到平面AB1C1
的距离等于点C到平面AB1C1的距离(5分)连结A1C交AC1
于H,∵ACC1A1是正方形,∴CH⊥AC1.∵B1C1⊥A1C1,B1C1
⊥CC1,∴B1C1⊥A1C1,B1C1⊥CC1,∴B1C1⊥平面ACC1A1.
∴B1C1⊥CH.∴CH⊥平面AB1C1,∴CH的长度为点C到平面AB1C1的距离.
∵ ∴点B到平面AB1C1的距离等于
∴点B到平面AB1C1的距离等于 (8分)
(8分)
(Ⅲ)取A1B1的中点D,连接C1D,∵△A1B1C1是等腰三角形,所以C1D⊥A1B1,又∵直三棱柱ABC-A1B1C1中,侧面A1B1BA⊥底面A1B1C1,∴C1D⊥侧面A1B1BA.作DE⊥AB1于E,;连C1E,则DE为C1E的平面A1B1BA内的射影,∴C1E⊥AB1
∴∠C1ED为二面角C1-AB1-A1的平面角.……………………(10分)
由已知C1D= ∴
∴ ,∴
,∴
即二面角C1-AB1-A1的大小为60°…………………………(12分)
 解法二:如图建立空间直角坐标系,依题意A(2,0,0),
解法二:如图建立空间直角坐标系,依题意A(2,0,0),
B(0,2,0),A1(2,0,2),B1(0,2,2),C1(0,0,2).(2分)
(Ⅰ)证明:
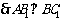
 …(4分)
…(4分)
(Ⅱ)设 的法向量,由
的法向量,由
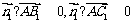 得
得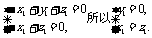 令
令
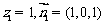 (6分),
(6分),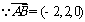 ,∴点B到平面
,∴点B到平面
AB1C1的距离 ……………………(8分)
……………………(8分)
(Ⅲ)解设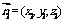 是平面A1AB1的法向量,由
是平面A1AB1的法向量,由
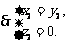 令
令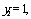 则
则 (10分),
(10分),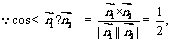
∴二面角C1-AB-A1的大小为60°.…………………………(12分)
18.[解析](1)设A通过体能射击反应分别记为事件M、N、P
则A能够入选包含的下几个互斥事件:
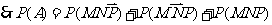
 (6分)
(6分)
(2) (12分)
(12分)
17.[解析](Ⅰ)由已知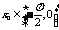 ,且
,且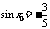 ,可得
,可得 ,
,
∴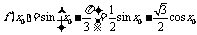 ,
,
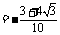 ; …(5分)
; …(5分)
(Ⅱ)将函数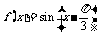 的图象向左平移
的图象向左平移 个单位,得
个单位,得 图象关于
图象关于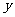 轴对称,∴
轴对称,∴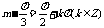 (7分),∴
(7分),∴ ,又∵
,又∵
∴ ,∴
,∴ .………………………(10分)
.………………………(10分)
16.[答案]25[解析]不等式表示的平面区域如图所示阴
影部分,当直线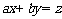 (a>0,b>0)过直线x-y+2=0与直
(a>0,b>0)过直线x-y+2=0与直
线3x-y-6=0的交点(4,6)时,目标函数 (a>0,b>0)取得最大12,∴4a+6b=12,即2a+3b=6.
(a>0,b>0)取得最大12,∴4a+6b=12,即2a+3b=6.
15.[答案] [解析]设球的内接正四棱锥的底面所在平面截球所得圆面的半径为
[解析]设球的内接正四棱锥的底面所在平面截球所得圆面的半径为 ,
,
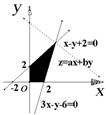 球的半径为
球的半径为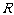 ,由
,由 ,于是
,于是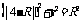
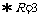
 .
.
14.[答案]-2[解析]由已知得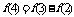

 =-2.
=-2.
13.[答案]560[解析]设含 的为第
的为第 项,
项,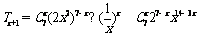 ,
,
令 得
得 ,故系数为
,故系数为 =560.
=560.
12.[答案]B[解析]过 作
作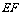 的垂线垂足为
的垂线垂足为 ,连结
,连结 ,则
,则 就是截面与
就是截面与
底面所成二面角的平面角 ,∴
,∴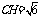 ,设
,设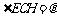 ,则
,则 ,
,
 ,
, ,
,
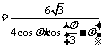
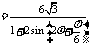 ,
, ,∴当
,∴当 或
或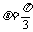 时,
时, 取得最大值
取得最大值 ,
,
此时 取得最大值
取得最大值 .
.
11.[答案]D[解析]将一条路经抽象为如下的一个排法(5-1)+(8-1)=11格:

其中必有四个“↑”和七个“→”组成! 所以四个“↑”和七个“→”的一个排序就对应一条路经,所以从A到B共有 条不同的路径.
条不同的路径.
10.[答案]C[解析]不妨设椭圆方程为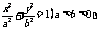 ,由题意可作草图:于是
,由题意可作草图:于是 ,而
,而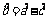 ,故
,故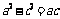 ,解得
,解得 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com