5．设为阿伏加德罗常数的值，下列叙述正确的是

A．常温下，的溶液中氮原子数为0.2

B．1mol羟基中电子数为10

C．在反应中，每生成3mol转移的电子数为6

D．常温常压下，22.4L乙烯中键数为4

4．下列有关物质的性质或应用的说法不正确的是

A．二氧化硅是生产光纤制品的基本原料

B．水玻璃可用于生产黏合剂和防火剂

C．盐析可提纯蛋白质并保持其生理活性

D．石油分馏可获得乙烯、丙烯和丁二烯

3．下列离子方程式表达正确的是

A．用惰性电极电解熔融氯化钠：

B．用氢氧化钠溶液除去铝表面的氧化膜：

C．用稀氢氧化钠溶液吸收二氧化氮：

D．用食醋除去水瓶中的水垢：

[答案]B

[解析]本题主要考查的是离子方程式的正误判断。A项，电解的是熔融状态的NaCl，不是NaCl溶液，2NaCl2Na + Cl₂↑；B项，Al2O3能溶于NaOH溶液，生成偏铝酸盐；C项，NO₂与NaOH反应，生成硝酸盐和亚硝酸盐，2OH^- + 2NO₂ = NO₃^- + NO₂^- + H₂O；D项，水垢中的主要成分为CaCO₃，是难溶物。综上分析可知，本题选B项。

2．水是最宝贵的资源之一。下列表述正确的是

A．H₂O的电子式为

B．4℃时，纯水的pH=7

C．中，质量数之和是质子数之和的两倍

D．273K、101kPa，水分子间的平均距离：(气态)＞(液态)＞(固态)

1．化学与能源开发、环境保护、资源利用等密切相关。下列说法正确的是

A．为提高农作物的产量和质量，应大量使用化肥和农药

B．绿色化学的核心是应用化学原理对环境污染进行治理

C．实现化石燃料清洁利用，就无需开发新能源

D．垃圾是放错地方的资源，应分类回收利用

23、(本小题满分10分)

已知△ABC的三边长都是有理数。

(1)求证cosA是有理数；(2)求证：对任意正整数n，cosnA是有理数。

[解析] 本题主要考查余弦定理、数学归纳法等基础知识，考查推理论证的能力与分析问题、解决问题的能力。满分10分。

(方法一)(1)证明：设三边长分别为，，∵是有理数，

是有理数，分母为正有理数，又有理数集对于除法的具有封闭性，

∴必为有理数，∴cosA是有理数。

(2)①当时，显然cosA是有理数；

当时，∵，因为cosA是有理数， ∴也是有理数；

②假设当时，结论成立，即coskA、均是有理数。

当时，，

，

，

解得：

∵cosA，，均是有理数，∴是有理数，

∴是有理数。

即当时，结论成立。

综上所述，对于任意正整数n，cosnA是有理数。

(方法二)证明：(1)由AB、BC、AC为有理数及余弦定理知

是有理数。

(2)用数学归纳法证明cosnA和都是有理数。

①当时，由(1)知是有理数，从而有也是有理数。

②假设当时，和都是有理数。

当时，由，

，

及①和归纳假设，知和都是有理数。

即当时，结论成立。

综合①、②可知，对任意正整数n，cosnA是有理数。

22、(本小题满分10分)

某工厂生产甲、乙两种产品，甲产品的一等品率为80%，二等品率为20%；乙产品的一等品率为90%，二等品率为10%。生产1件甲产品，若是一等品则获得利润4万元，若是二等品则亏损1万元；生产1件乙产品，若是一等品则获得利润6万元，若是二等品则亏损2万元。设生产各种产品相互独立。

(1)记X(单位：万元)为生产1件甲产品和1件乙产品可获得的总利润，求X的分布列；

(2)求生产4件甲产品所获得的利润不少于10万元的概率。

[解析] 本题主要考查概率的有关知识，考查运算求解能力。满分10分。

解：(1)由题设知，X的可能取值为10，5，2，-3，且

　　 P(X=10)=0.8×0.9=0.72，　　　　　　　 P(X=5)=0.2×0.9=0.18，

　　 P(X=2)=0.8×0.1=0.08，　　　　　　　 P(X=-3)=0.2×0.1=0.02。

　 由此得X的分布列为：

(2)设生产的4件甲产品中一等品有件，则二等品有件。

　　 由题设知，解得，

　　 又，得，或。

所求概率为

答：生产4件甲产品所获得的利润不少于10万元的概率为0.8192。

21.[选做题]本题包括A、B、C、D四小题，请选定其中两题，并在相应的答题区域内作答。若多做，则按作答的前两题评分。解答时应写出文字说明、证明过程或演算步骤。

A．　　 选修4-1：几何证明选讲

(本小题满分10分)

AB是圆O的直径，D为圆O上一点，过D作圆O的切线交AB延长线于点C，若DA=DC，求证：AB=2BC。

[解析] 本题主要考查三角形、圆的有关知识，考查推理论证能力。

(方法一)证明：连结OD，则：OD⊥DC，

又OA=OD，DA=DC，所以∠DAO=∠ODA=∠DCO，

∠DOC=∠DAO+∠ODA=2∠DCO，

所以∠DCO=30⁰，∠DOC=60⁰，

所以OC=2OD，即OB=BC=OD=OA，所以AB=2BC。

(方法二)证明：连结OD、BD。

因为AB是圆O的直径，所以∠ADB=90⁰，AB=2 OB。

因为DC 是圆O的切线，所以∠CDO=90⁰。

又因为DA=DC，所以∠DAC=∠DCA，

于是△ADB≌△CDO，从而AB=CO。

即2OB=OB+BC，得OB=BC。

故AB=2BC。

B．　　 选修4-2：矩阵与变换

(本小题满分10分)

在平面直角坐标系xOy中，已知点A(0,0)，B(-2,0)，C(-2,1)。设k为非零实数，矩阵M=,N=，点A、B、C在矩阵MN对应的变换下得到点分别为A₁、B₁、C₁，△A₁B₁C₁的面积是△ABC面积的2倍，求k的值。

[解析] 本题主要考查图形在矩阵对应的变换下的变化特点，考查运算求解能力。满分10分。

解：由题设得

由，可知A₁(0，0)、B₁(0，-2)、C₁(，-2)。

计算得△ABC面积的面积是1，△A₁B₁C₁的面积是，则由题设知：。

所以k的值为2或-2。

C．　　 选修4-4：坐标系与参数方程

(本小题满分10分)

在极坐标系中，已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切，求实数a的值。

[解析] 本题主要考查曲线的极坐标方程等基本知识，考查转化问题的能力。满分10分。

解：，圆ρ=2cosθ的普通方程为：，

直线3ρcosθ+4ρsinθ+a=0的普通方程为：，

又圆与直线相切，所以解得：，或。

D．　　 选修4-5：不等式选讲

(本小题满分10分)

设a、b是非负实数，求证：。

[解析] 本题主要考查证明不等式的基本方法，考查推理论证的能力。满分10分。

(方法一)证明：

因为实数a、b≥0，

所以上式≥0。即有。

(方法二)证明：由a、b是非负实数，作差得

当时，，从而，得；

当时，，从而，得；

所以。

[必做题]第22题、第23题，每题10分，共计20分。请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤。

20、(本小题满分16分)

设是定义在区间上的函数，其导函数为。如果存在实数和函数，其中对任意的都有>0，使得，则称函数具有性质。

(1)设函数，其中为实数。

(i)求证：函数具有性质； (ii)求函数的单调区间。

(2)已知函数具有性质。给定设为实数，

，，且，

若||<||，求的取值范围。

[解析] 本小题主要考查函数的概念、性质、图象及导数等基础知识，考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力。满分16分。

(1)(i)

∵时，恒成立，

∴函数具有性质；

(ii)(方法一)设，与的符号相同。

当时，，，故此时在区间上递增；

当时，对于，有，所以此时在区间上递增；

当时，图像开口向上，对称轴，而，

对于，总有，，故此时在区间上递增；

(方法二)当时，对于，

　 所以，故此时在区间上递增；

当时，图像开口向上，对称轴，方程的两根为：，而

　当时，，，故此时在区间　　 上递减；同理得：在区间上递增。

综上所述，当时，在区间上递增；

　　　　　 当时，在上递减；在上递增。

(2)(方法一)由题意，得：

又对任意的都有>0，

所以对任意的都有，在上递增。

又。

当时，，且，

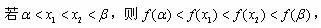
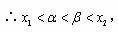
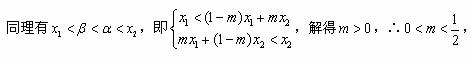
综合以上讨论，得：所求的取值范围是(0，1)。

(方法二)由题设知，的导函数，其中函数对于任意的都成立。所以，当时，，从而在区间上单调递增。

①当时，有，

，得，同理可得，所以由的单调性知、，

从而有||<||，符合题设。

②当时，，

，于是由及的单调性知，所以||≥||，与题设不符。

③当时，同理可得，进而得||≥||，与题设不符。

因此综合①、②、③得所求的的取值范围是(0，1)。

数学Ⅱ(附加题)

19、(本小题满分16分)

设各项均为正数的数列的前n项和为，已知，数列是公差为的等差数列。

(1)求数列的通项公式(用表示)；

(2)设为实数，对满足的任意正整数，不等式都成立。求证：的最大值为。

[解析] 本小题主要考查等差数列的通项、求和以及基本不等式等有关知识，考查探索、分析及论证的能力。满分16分。

(1)由题意知：，

，

化简，得：

，

当时，，适合情形。

故所求

(2)(方法一)

， 恒成立。

　 又，，

故，即的最大值为。

(方法二)由及，得，。

于是，对满足题设的，，有

。

所以的最大值。

另一方面，任取实数。设为偶数，令，则符合条件，且。

于是，只要，即当时，。

所以满足条件的，从而。

因此的最大值为。