1．熟练、扎实地掌握基础知识、基本技能和基本方法是转化的基础；丰富的联想、机敏细微的观察、比较、类比是实现转化的桥梁；培养训练自己自觉的化归与转化意识需要对定理、公式、法则有本质上的深刻理解和对典型习题的总结和提炼，要积极主动有意识地去发现事物之间的本质联系。“抓基础，重转化”是学好中学数学的金钥匙。

例1．某厂2001年生产利润逐月增加，且每月增加的利润相同，但由于厂方正在改造建设，元月份投入资金建设恰好与元月的利润相等，随着投入资金的逐月增加，且每月增加投入的百分率相同，到12月投入建设资金又恰好与12月的生产利润相同，问全年总利润m与全年总投入N的大小关系是　　　　　　　 (　 )

A. m>N　　　 　B. m<N　　 　　C.m=N　　 　　D.无法确定

[分析]每月的利润组成一个等差数列{a_n}，且公差d＞0，每月的投资额组成一个等比数列{b_n}，且公比q＞1。，且，比较与的大小。

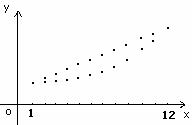
若直接求和，很难比较出其大小，但注意到等差数列的通项公式a_n=a₁+(n-1)d是关于n的一次函数，其图象是一条直线上的一些点列。等比数列的通项公式b_n=a₁q^n-1是关于n的指数函数，其图象是指数函数上的一些点列。

在同一坐标系中画出图象，直观地可以看出a_i≥b_i 　则＞，即m＞N。

[点评]把一个原本是求和的问题，退化到各项的逐一比较大小，而一次函数、指数函数的图象又是每个学生所熟悉的。在对问题的化归过程中进一步挖掘了问题的内涵，通过对问题的反思、再加工后，使问题直观、形象，使解答更清新。

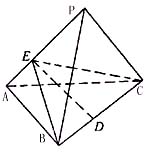
例2．如果，三棱锥P-ABC中，已知PA⊥BC，PA=BC=l，PA，BC的公垂线ED=h．求证三棱锥P-ABC的体积．

分析：如视P为顶点，△ABC为底面，则无论是S_△ABC以及高h都不好求．如果观察图形，换个角度看问题，创造条件去应用三棱锥体积公式，则可走出困境．

解：如图，连结EB，EC，由PA⊥BC，PA⊥ED，ED∩BC=E，可得PA⊥面ECD．这样，截面ECD将原三棱锥切割成两个分别以ECD为底面，以PE、AE为高的小三棱锥，而它们的底面积相等，高相加等于PE+AE=PA=l，所以

V_P－ABC=V_P－ECD+V_A－ECD=S_△ECD•AE+S_△ECD•PE=S_△ECD •PA=•BC·ED·PA=． 　 评注：辅助截面ECD的添设使问题转化为已知问题迎刃而解．

例3．在的展开式中x的系数为( )．

(A)160　　　　　　 (B)240　　　　　　　 (C)360　　　　　 (D)800

分析与解：本题要求展开式中x的系数，而我们只学习过多项式乘法法则及二项展开式定理，因此，就要把对x系数的计算用上述两种思路进行转化：

思路1：直接运用多项式乘法法则和两个基本原理求解，则展开式是一个关于x的10次多项式， =(x²+3x+2) (x²+3x+2) (x²+3x+2) (x²+3x+2) (x²+3x+2)，它的展开式中的一次项只能从5个括号中的一个中选取一次项3x并在其余四个括号中均选 择常数项2相乘得到，故为·(3x)··2⁴=5×3×16x=240x，所以应选(B)．

思路2 利用二项式定理把三项式乘幂转化为二项式定理再进行计算，∵x²+3x+2=x²+ (3x+2)=(x²+2)+3x=(x²+3x)+2=(x+1)(x+2)=(1+x)(2+x)，∴这条思路下又有四种不同的化归与转化方法．①如利用x²+3x+2=x²+(3x+2)转化，可以发现只有(3x+2)⁵中会有x项，即(3x)·2⁴=240x，故选(B)；②如利用x²+3x+2= (x²+2)+3x进行转化，则只 (x²+2) ⁴·3x中含有x一次项，即·3x·C₄⁴·2⁴=240x；③如利用x2+3x+2=(x2+3x)+2进行转化，就只有·(x²+3x)·2⁴中会有x项，即240x；④如选择x²+3x+2=(1+x)(2+x)进行转化，=×展开式中的一次项x只能由(1+x)⁵中的一次项乘以(2+x)⁵展开式中的常数项加上(2+x)⁵展开式中的一次项乘以(1+x)⁵展开式中的常数项后得到，即为x·2⁵+•2⁴•x••1⁵=160x+80x=240x，故选(B)．　

评注：化归与转化的意识帮我们把未知转化为已知。

例4．若不等式对一切均成立，试求实数的取值范围。

解：　　　 _[来源:]

令，则要使它对均有，只要有

　　　　 或。

点评：在有几个变量的问题中，常常有一个变元处于主要地位，我们称之为主元，由于思维定势的影响，在解决这类问题时，我们总是紧紧抓住主元不放，这在很多情况下是正确的。但在某些特定条件下，此路往往不通，这时若能变更主元，转移变元在问题中的地位，就能使问题迎刃而解。本题中，若视x为主元来处理，既繁且易出错，实行主元的转化，使问题变成关于p的一次不等式，使问题实现了从高维向低维转化，解题简单易行。

4．化归与转化应遵循的基本原则：

(1)熟悉化原则：将陌生的问题转化为熟悉的问题，以利于我们运用熟知的知识、经验和问题来解决。

(2)简单化原则：将复杂的问题化归为简单问题，通过对简单问题的解决，达到解决复杂问题的目的，或获得某种解题的启示和依据。

(3)和谐化原则：化归问题的条件或结论，使其表现形式更符合数与形内部所表示的和谐的形式，或者转化命题，使其推演有利于运用某种数学方法或其方法符合人们的思维规律。

(4)直观化原则：将比较抽象的问题转化为比较直观的问题来解决。

(5)正难则反原则：当问题正面讨论遇到困难时，可考虑问题的反面，设法从问题的反面去探求，使问题获解。

3．转化有等价转化和非等价转化。等价转化前后是充要条件，所以尽可能使转化具有等价性；在不得已的情况下，进行不等价转化，应附加限制条件，以保持等价性，或对所得结论进行必要的验证。

2．化归与转化思想的实质是揭示联系，实现转化。除极简单的数学问题外，每个数学问题的解决都是通过转化为已知的问题实现的。从这个意义上讲，解决数学问题就是从未知向已知转化的过程。化归与转化的思想是解决数学问题的根本思想，解题的过程实际上就是一步步转化的过程。数学中的转化比比皆是，如未知向已知转化，复杂问题向简单问题转化，新知识向旧知识的转化，命题之间的转化，数与形的转化，空间向平面的转化，高维向低维转化，多元向一元转化，高次向低次转化，超越式向代数式的转化，函数与方程的转化等，都是转化思想的体现。

1．解决数学问题时，常遇到一些问题直接求解较为困难，通过观察、分析、类比、联想等思维过程，选择运用恰当的数学方法进行变换，将原问题转化为一个新问题(相对来说，对自己较熟悉的问题)，通过新问题的求解，达到解决原问题的目的，这一思想方法我们称之为“化归与转化的思想方法”。

(十)1、字数：一是字数不足往往被认为文章内容单薄，分数很难上档次；二是字数太多。洋洋洒洒千字以上，给人一种臃肿的感觉，阅卷者一看这种文章就反感，这样的作文得分高低就可想而知。

2、书写：书写要认真。不要写草字，以免妨碍辨认。标点的书写也要规范，特别注意以下三点：

(1)一行之首不要出现句号、逗号、问号、叹号、顿号、分号。可以把这些符号挤在前一行的末尾。

(2)引号、括号、书名号前半不出现在一行之末，可以在这些符号后面挤着写一个字。引号、括号、书名号后一半不出现在一行之首，可以把这些符号挤在上一行之末。

(3)省略号、破折号占两个格，不能断开，写不下时挤在一行之末。

附：2009高考作文评分标准

说明：

　1、基础等级评分，内容以“题意”、“中心”为重点，表达以“语言”、“文体” 为重点。

2、发展等级评分，以“有文采”、“有创意”为重点。

3、发展等级，用一点评分法，即发展等级中的一点特突出，这个等级即可给满分或高分；有一点较突出，可打二类；句子通顺，找不到突出的地方，打三类。只要能找到有发展等级的，就给这一块得分。

4、有铁证是抄袭的，发展等级给0分。

5、不跨类打分，即内容表达发展三者中有一点是一类，另两点不能低于二类。

总体评分原则：给分有理，扣分有据，宽严有度，公平合理。总体分为四类：一类：60-50分，以55分为中间线；二类：49-43分，以46分为中间线；三类：42-36分，以39分为中间线；四类：35分以下。

扣分标准：

　 关于字数问题：

(1)不足400字，不成文章，参照四等作文打分，内容表达不得超5分，不给发展等级分，最高不超10分；

(2)超400字不到800字，表达扣分，内容、特征都扣，少50字扣1分，80亦扣1分。不到100个字不准扣2分，无标题扣2分，错别字每个扣1分，重复不计扣至20分为止。标点错三处扣1分。一点到底看作标点错误要从严，但逗号、句号两可的不扣。　

关于发展等级：

(1)深刻、丰富、有创意原则上与基础等级判分相互联系，两者不可分离，前者高后者才高；

(2)基本合立意的发展等级最多只能是二等，可三等，不可一等；

(3)偏离题意，抄袭作文等，发展等级不给分。

(九)综合运用多种表达方式。后期备考阶段不妨训练写信，因为写信可以记叙、议论、抒情、编故事，而且还是应用文。另外，要把每一段的首句写好。每一段的首句犹如人的眉目，把首句写好，“眉清目秀”，整个段落都显着精神。“写好”，包含两层意思，一是字要写好不涂抹，二是写成提摄全段大意的中心句。

(八)文章结尾三注意一要求：结尾是全文的归纳，不是重复前文；注意提高引申；结尾要有力(画龙点睛，发人深思；总结全文，照应开头；叙述结束，自然收尾；抒发情感，引起共鸣)，要给人以回味激励，启发和思考，即要有“撞钟”效应。结尾的方法也很多：总结全文，以揭示主旨；展示未来，以鼓舞斗志；抒发情怀，以增强文章感染力；造语含蓄，让阅卷者掩卷而思遐想不已。

(七)谋篇布局的要领：袖手于前，成竹在胸，疾书于后，一气呵成(凤头、猪肚、豹尾)。