
1、北京市在全国率先推出“一元节能灯”计划,以财政补贴方式推广500万只节能灯,按7角或1元的超低价格向居民出售。北京市民觉得节能灯价格便宜,又能节省电费,于是纷纷抢购。这表明,居民购物
A、考虑供给与需求的统一 B、考虑国家政策与家庭实际的统一
C、只考虑价格因素
D、考虑使用价值与价值的统一
22. (本小题满分12分)
已知函数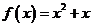 。
。
(I)数列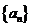 满足
满足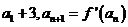 ,求数列
,求数列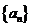 的通项公式;
的通项公式;
(II)数列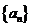 满足:
满足: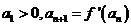 ,若
,若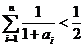 对任意的
对任意的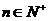 恒成立,试求
恒成立,试求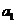 的取值范围;
的取值范围;
(III)数列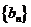 满足:
满足: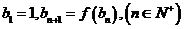 ,记
,记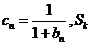 为数列
为数列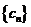 的前
的前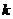 项和,
项和,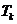 为数列
为数列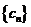 的前
的前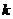 项积。
项积。
(文)比较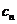 与
与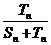 的大小
的大小
(理)证明: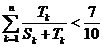 。
。




21. (本小题满分12分)
(文)设函数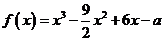 。
。
(I)对于任意实数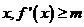 恒成立,求实数
恒成立,求实数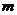 的最大值;
的最大值;
(II)若方程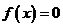 有且仅有一个实根,求实数
有且仅有一个实根,求实数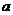 的取值范围;
的取值范围;
(理)已知函数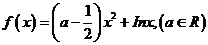
(I)当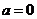 时,求
时,求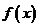 在区间
在区间 上的最大值和最小值;
上的最大值和最小值;
(II)在区间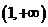 上,若
上,若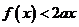 恒成立,求
恒成立,求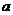 的取值范围。
的取值范围。
20. (本小题满分12分)
已知二次函数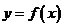 的图象经过坐标原点,其导函数为
的图象经过坐标原点,其导函数为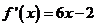 ,数列
,数列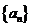 的前
的前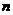 项和为
项和为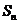 ,点
,点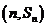
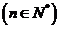 均在函数
均在函数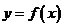 的图像上。
的图像上。
(I)求数列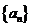 的通项公式;
的通项公式;
(II)设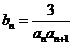 ,
,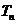 是数列
是数列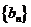 的前
的前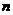 项和,求使得
项和,求使得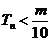 对所有
对所有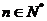 都成立的最小正整数
都成立的最小正整数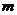 。
。
19. (本小题满分12分)
设函数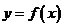 是定义在
是定义在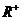 上的函数,并且满足下面三个条件:(1)对正数
上的函数,并且满足下面三个条件:(1)对正数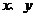 都有
都有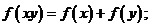 (2)当
(2)当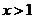 时,
时,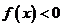 ;(3)
;(3)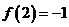 。
。
(I)求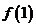 和
和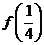 的值;
的值;
(II)判断函数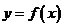 的单调性,并证明。
的单调性,并证明。
(III)(文)如果不等式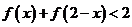 成立,求
成立,求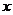 的取值范围。
的取值范围。
(理)如果存在正数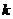 ,使不等式
,使不等式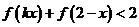 有解,求正数
有解,求正数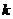 的取值范围。
的取值范围。
18. (本小题满分12分)
用长为24m的钢条围成一个长方体性状的框架,要求长方体的长与宽之比为3:1,问该长方体长、宽、高各为多少时,其体积最大?最大体积是所少?
17. (本小题满分10分)
已知函数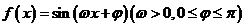 为偶函数,且其图像上相邻的一个最高点和最低点之间的距离为
为偶函数,且其图像上相邻的一个最高点和最低点之间的距离为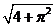 。
。
(I)求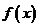 的解析式;
的解析式;
(II)若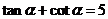 ,求
,求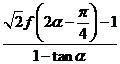 的值。
的值。
16. 已知某型号进口仪器每台降价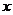 成(1成为10%),那么售出数量就增加
成(1成为10%),那么售出数量就增加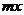 成(
成(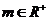 常数),当某商场定价为每台
常数),当某商场定价为每台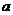 元时,售出
元时,售出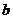 台,设降价后的营业额
台,设降价后的营业额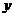 是每台降价
是每台降价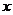 成的函数,当
成的函数,当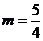 时,每台降价
成时,营业额
时,每台降价
成时,营业额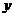 最大,最大值为 元。
最大,最大值为 元。
15.已知函数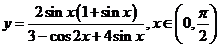 ,则它的值域为 。
,则它的值域为 。
14. (文)曲线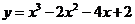 在点
在点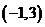 处的切线方程是
。
处的切线方程是
。
(理)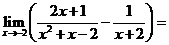
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com