3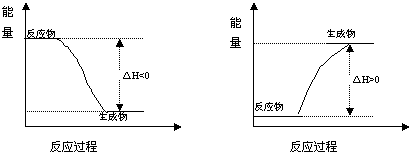．化学反应中的能量变化示意图对于该“示意图”可理解为下列形式：

　 由能量守恒可得：

　反应物的总能量：生成物的总能量+热量(放热反应)

　　 反应物的总能量：生成物的总能量-热量(吸热反应)

2．放热反应和吸热反应

　 (1)放热反应：即有热量放出的化学反应，其反应物的总能量大于生成物的总能量。

(2)吸热反应：即吸收热量的化学反应，其反应物的总能量小于生成物的总能量。

1．化学反应及其能量变化

　 任何一个化学反应中，反应物所具有的总能量与生成物所具有的总能量总不会相等的。在新物质产生的同时总是伴随着能量的变化。

热点题型1：绝对值不等式的解法：

例1(2005年全国卷Ⅱ.17)设函数 ，求使 的x的取值范围。

解：由于 是增函数， 等价于 ………………..(1)

(ⅰ)当 ， (1)式恒成立。

(ⅱ)当 ，(1)式化为 。

(ⅲ)当 ，(1)式无解。

综上，x的取值范围是 。

变式1：已知实数a满足不等式 ，解关于x的不等式： 。

热点题型2：含参的分式不等式的解法：

例2(2005年江西.17)已知函数 ，且方程 有两个实根为 。

(1)　　　 求函数 的解析式；

(2)　　　 设 ，解关于x的不等式： 。

解：(1)将 分别代入方程 ，

所以 。

(2)不等式即为 ，

即 。

(ⅰ)当

(ⅱ)当

(ⅲ)当 。

变式2：解关于x的不等式

热点题型3：不等式的证明在数列等章节中的运用：

例3：(2005年全国卷Ⅰ.19)设等比数列 的公比为q，前n项和

(1)　　　 求q的取值范围

(2)　　　 设

解：(ⅰ)因为 是等比数列， ，可得

当

上式等价于不等式组

解(1)得q＞1；解(2)，由于n可为奇数，可为偶数，得－1＜q＜1。

综上，q的取值范围是 。

(ⅱ)由

于是

又因为 ，且－1＜q＜0或q>0,所以，

变式3：已知数列 的通项公式 ，求函数 。

热点题型4：不等式在解析几何中的运用：

例4：(2005年天津.20)某人在一山坡P处观看对面山顶上的一座铁塔，如图所示。塔高BC＝80(米)，塔所在的山高OB＝220(米)，OA＝200(米)，图中所示的山坡可视为直线 且点P在直线 上， 与水平地面的夹角为 。试问此人距水平地面多高时，观看塔的视角 最大(不计此人的身高)？(图见教材P47页)

解：如图所示，建立平面直角坐标系，则A(200，0)，B(0，220)，C(0，300)，

直线 的方程为

设点P的坐标为 ，由经过两点的直线的斜率公式。

由直线PC到直线PB的角的公式得

＝

要使 达到最大，只需 达到最小，由圴值不等式。

时上式取得等号，故当x＝320时tanBPC最大。这时，点P的纵坐标y为

由此实际问题知，0＜ ＜ ，所以tanBPC最大时， 最大，故当此人距水平地面60米高时，观看铁塔的视角 最大。

变式4：已知椭圆 的方程为 双曲线 的方程为 若直线 与椭圆 及双曲线 都恒有两个不同的交点为，且 与 的两个交点A和B满足 (其中O为原点)，求k的取值范围。

四：课堂小结：

五：作业。

2、　 不等式在函数、数列、导数、解析几何、三角函数等的广泛运用。

1、　 解含参数的分式不等式和绝对值不等式。

25．《好吃的苹果平凡的脸》中有这么一段话：“许多日子以来，我嘴里衔着一枚青橄榄，酸酸的、涩涩的、而此时却嚼出了丝丝甘甜。”

其实，每个人在成长的道路上，又何尝常有“衔过青橄榄”呢？在你克服各种各样的困难的过程中，或者在你完成挑战性任务的过程中，或者在你消除误解赢得信任的过程中，或者在你努力改变自己处境的过程中……你不也有过艰辛、有过苦涩吗？不也尝到过丝丝甘甜吗？

联系实际，以“我也衔过一枚青橄榄”为题，写一篇800字左右的记叙文。

24．你知道下面的惯用语是什么吗？(2分) ①、把混混噩噩、不明事理的人喻为(　　　　　 　) ②、把技艺不精、勉强凑合的人喻为(　　　　　 　)

23．续写句子。(3分)

一位心理保健教师应邀给少年犯上课，走向讲台时不小心摔了一跤，引起哄堂大笑。这位教师不慌不忙站起来，脸朝着大家笑： 　　　　　　　　　　　　　　　　　。

请在横线上补出这位教师说的话，要求适合特定的场合和对象，体现幽默的风格，不超过35个字。

22．读下面一则材料，从中你有什么发现?写出你的探究结果。(3分)

　　 美国生物学家曾做过这样的实验：将初生的婴儿分成四组，一组听不到任何声音；二组播放录制的催眠曲；三组用节拍器仿声；四组播放母亲心跳的录音。结果表明，第四组仅用了其他三组所用时间的一半，婴儿就安安稳稳地睡着了，而第一组的婴儿在长达60%的时间内都在啼哭，骚动。

　　　 探究结果：