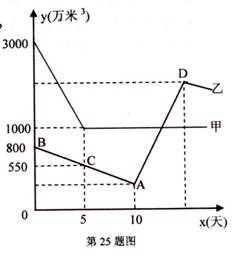
25．(本小题满分8分)因南方旱情严重，乙水库的蓄水量以每天相同的速度持续减少．为缓解旱情，北方甲水库立即以管道运输的方式给予以支援下图是两水库的蓄水量y(万米³)与时间x(天)之间的函数图象．在单位时间内，甲水库的放水量与乙水库的进水量相同(水在排放、接收以及输送过程中的损耗不计)．通过分析图象回答下列问题：

　 (1)甲水库每天的放水量是多少万立方米？

　 (2)在第几天时甲水库输出的水开始注入乙水库？此时乙水库的蓄水量为多少万立方米？

　 (3)求直线AD的解析式．

解析：

答案：解：(1)甲水库每天的放水量为(3000－1000)÷5＝400(万米³/天)……………………1分

(2)甲水库输出的水第10天时开始注入乙水库………………………………………1分

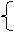∴­　　　　　　　　 ∴k＝－50　　 b＝800　　 ………………………………1分

∴直线AB的解析式为：y_AB＝－50x+800　 ……………………………………1分

当x＝10时，y＝300　 ∴此时乙水库的蓄水量为300(万米³) ………………1分

(3)∵甲水库单位时间的放水量与乙水库单位时间的进水量相同且损耗不计

∴乙水库的进水时间为5天

∵乙水库15天后的蓄水量为：300+(3000－1000) －50×5＝2050(万米³) …1分

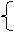∴­　　　　　　　　 ∴k₁＝350　　 b₁＝－3200　　 ………………………………1分

∴直线AD的解析式为：y_AD＝350x－3200　 ……………………………………1分

点评：

　　　　　　　 ∴点P(－2,3)在这个二次函数的图象上…………………………1分

　　　　　　　 ∵－x²－2x+3＝0

　　　　　　　 ∴x₁＝－3，x₂＝1　 ∴与轴的交点为：(－3,0)，(1,0)…………1分

　　　　　　　 S_△PAB＝×4×3＝6 …………………………………………………1分

24．(本小题满分7分) ．某区对参加2010年中考的5000名初中毕业生进行了一次视力抽样调查，绘制出频分布表和频数分布直方图的一部分．请根据图表信息回答下列问题：

　 (1)在频数分布表中，a的值为__________，b的值为__________，并将频数分布直方图补充完整；

　 (2)甲同学说“我的视力情况是此次抽样调查所得数据的中位数”，问甲同学的视力情况应在什么范围内？

　 (3)若视力在4.9以上(含4.9)均属正常，则视力正常的人数占被统计人数的百分比是__________，并根据上述信息估计全区初中毕业生中视力正常的学生有多少人？

视力	频数(人)	频率
4.0≤x＜4.3	20	0.1
4.3≤x＜4.6	40	0.2
4.6≤x＜4.9	70	0.35
4.9≤x＜5.2	a	0.3
5.2≤x＜5.5	10	b

答案：(1)a＝60，b＝0.05 …………………………………………………………………1分

　　　　　 补全直方图 ………………………………………………………………………1分

(2)甲同学的视力情况范围：4.6≤x＜4.9…………………………………………1分

(3)视力正常的人数占被统计人数的百分比是：×100%＝35%　 ………1分

　　 全区初中毕业生中视力正常的学生约有：5000×35%＝1750(人) …………1分

23．(本小题满分6分) ．已知二次函数的图象经过点(0,3)，(－3,0)，(2, －5)，且与x轴交于A、B两点．

　 (1)试确定此二次函数的解析式；

　 (2)判断点P(－2,3)是否在这个二次函数的图象上？如果在，请求出△PAB的面积；如果不在，试说明理由．

答案：解：(1)设二次函数的解析式为y＝ax²+bx+c

　　　　　　　 ∵二次函数的图象经过点(0,3)，(－3,0)，(2, －5)

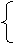　　　　　　　　　 c＝3

∴　 9a-3b+c＝0…………………………………………………2分

4a+2b+c＝－5

　　　　　　　 a＝－1，b＝－2，c＝3，y＝－x²－2x+3 …………………………1分

22．(本小题满分6分) 每个小方格都是边长为1个单位长度的小正方形，菱形OABC在平面直角坐标系中的位置如图所示．

(1)将菱形OABC先向右平移4个单位，再向上平移2个单位，得到菱形OA₁B₁C₁，请画出菱形OA₁B₁C₁，并直接写出点B₁的坐标；

(2)将菱形OABC绕原点O顺时针旋转90º，得到菱形OA₂B₂C₂，请画出菱形OA₂B₂C₂，并求出点B旋转到B₂的路径长．

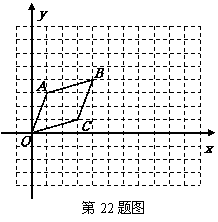
答案：(1)正确画出平移后图形…………………………1分

B₁(8,6)………………………………………1分

　　 (2)正确画出旋转图形……………………………1分

　　　　　 OB＝＝＝4……………………1分

BB₂的弧长＝＝2π…………………………2分

21．(本小题满分5分)先化简：(a － )÷ ，然后给a选择一个你喜欢的数代入求值．

答案：解：原式＝÷ …………………………1分

＝×……………………2分

＝(1－a) …………………………………………1分

(a取-1，1，0以外的任何数，计算正确均可得分)……1分

20．如图，在平面直角坐标系中，边长为1的正方形OA₁B₁C的对角线A₁C和OB₁交于点M₁；以M₁A₁为对角线作第二个正方形A₂A₁B₂ M₁，对角线A₁ M₁和A₂B₂ 交于点M₂；以M₂A₁为对角线作第三个正方形A₃A₁B₃ M₂，对角线A₁ M₂和A₃B₃ 交于点M₃；……，依次类推，这样作的第n个正方形对角线交点的坐标为M_n_______________．

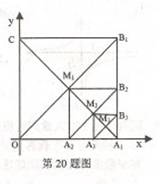
答案：(1－,)或另一书写形式(,)

19．已知关于x的分式方程 ＝1的解是非正数，则a的取值范围是_______________．

答案：a≤－1且a≠－2

18．Rt△ABC中，∠BAC＝90º，AB＝AC＝2，以AC为一边，在△ABC外部作等腰直角三角形ACD，则线段BD的长为_______________．

答案：4或2或(答对一值得1分，多答不得分)

17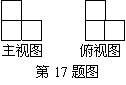．由一些完全相同的小正方体的搭成的几何体的主视图和俯视图如图所示，

则组成这个几何体的小正方体的个数可能是_______________．

答案：4或5(答对一值得1分，多答不得分)

16．代数式3x²－4x－5的值为7，则x²－ x－5的值为_______________．

答案：－1