
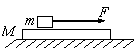
4.如图所示,质量为m的木块在质量为M的长木板上受到向右的拉力F的作用向右滑行,长木板处于静止状态,已知木块与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数为μ2。下列说法正确的是 ( )
 A.木板受到地面的摩擦力的大小一定是μ1mg
A.木板受到地面的摩擦力的大小一定是μ1mg
B.木板受到地面的摩擦力的大小一定是μ2(m+M)g
C.当F>μ2(m+M)g时,木板便会开始运动
D.无论怎样改变F的大小,木板都不可能运动
3.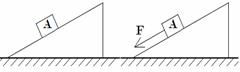 如图所示,斜面固定在水平地面上,先让物体A沿斜面下滑,恰能匀速.后给A一个沿斜面向下的力F,让其加速下滑.设前后两次A与斜面间的摩擦力分别为f1、f2,地面给斜面的支持力分别为N1、N2,则 (
)
如图所示,斜面固定在水平地面上,先让物体A沿斜面下滑,恰能匀速.后给A一个沿斜面向下的力F,让其加速下滑.设前后两次A与斜面间的摩擦力分别为f1、f2,地面给斜面的支持力分别为N1、N2,则 (
)
A.f1=f2 ,N1=N2 B.f1=f2 ,N1>N2
C.f1<f2 ,N1<N2 D.f1>f2 ,N1>N2
1.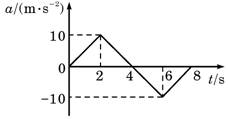 如图所示是某物体做直线运动的速度图象,下列有关物体运动情况判断正确的是( )
如图所示是某物体做直线运动的速度图象,下列有关物体运动情况判断正确的是( )
A.前两秒加速度为5 m/s2
B.4 s末物体回到出发点
C.6 s末物体距出发点最远
D.8 s末物体距出发点最远
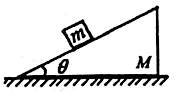 2.如图所示,物体m与斜面体M一起静止在水平面上。若将斜面的倾角θ稍微增大一些,且物体m仍静止在斜面上,则( )
2.如图所示,物体m与斜面体M一起静止在水平面上。若将斜面的倾角θ稍微增大一些,且物体m仍静止在斜面上,则( )
A.斜面体对物体的支持力变小
B.斜面体对物体的摩擦力变大
C.水平面与斜面体间的摩擦力变大
D.水平面与斜面体间的摩擦力变小
16.已知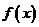 是以2为周期的偶函数,当
是以2为周期的偶函数,当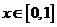 时,
时,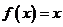 ,且在
,且在 内,关于
内,关于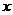 的方程
的方程 有四个根,则
有四个根,则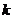 得取值范围是
得取值范围是 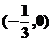
三 解答题
17记关于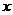 的不等式
的不等式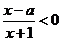 的解集为
的解集为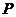 ,不等式
,不等式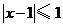 的解集为
的解集为 .
.
(1)若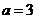 ,求
,求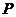 ;
;
(2)若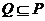 ,求正数
,求正数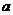 的取值范围
的取值范围
17解:(1)由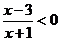 ,得
,得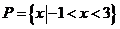 .
.
(2) .
.
由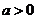 ,得
,得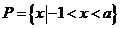 ,又
,又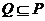 ,所以
,所以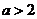 ,
,
即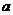 的取值范围是
的取值范围是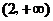 .
.
18设p:实数x满足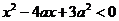 ,其中
,其中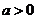 ,命题
,命题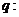 实数
实数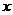 满足
满足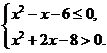 .
.
(Ⅰ)若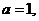 且
且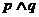 为真,求实数
为真,求实数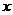 的取值范围;
的取值范围;
(Ⅱ)若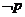 是
是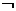
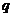 的充分不必要条件,求实数
的充分不必要条件,求实数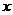 的取值范围.
的取值范围.
18解:由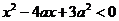 得
得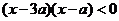 ,
,
又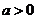 ,所以
,所以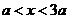 ,
,
当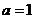 时,1<
时,1<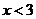 ,即
,即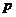 为真时实数
为真时实数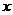 的取值范围是1<
的取值范围是1<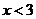 .
.
由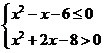 ,得
,得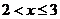 ,即
,即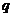 为真时实数
为真时实数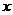 的取值范围是
的取值范围是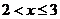 .
.
若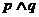 为真,则
为真,则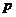 真且
真且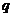 真,
真,
所以实数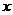 的取值范围是
的取值范围是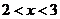 .
.
(Ⅱ) 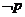 是
是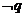 的充分不必要条件,即
的充分不必要条件,即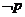
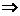
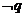 ,且
,且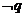
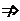
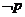 ,
,
设A=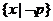 ,B=
,B=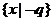 ,则
,则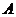
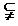
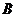 ,
,
又A=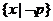 =
=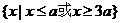 , B=
, B=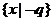 =
=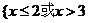 },
},
则0<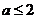 ,且
,且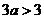
所以实数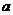 的取值范围是
的取值范围是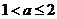 .
.
19两个二次函数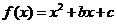 与
与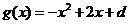 的图象有唯一的公共点
的图象有唯一的公共点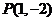 ,
,
(1)求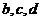 的值;
的值;
(2)设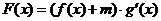 ,若
,若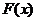 在
在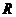 上是单调函数,求
上是单调函数,求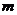 的范围,并指出是单调递增函数,还是单调递减函数。
的范围,并指出是单调递增函数,还是单调递减函数。
19解:(1)由已知得
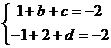 化简得
化简得 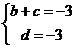
且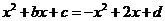
即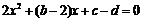 有唯一解
有唯一解
所以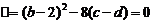
即 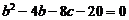
消去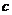 得
得 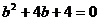 ,
,
解得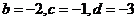
(2)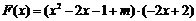

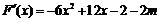
若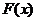 在
在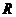 上为单调函数,则
上为单调函数,则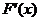 在
在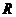 上恒有
上恒有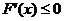 或
或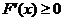 成立。
成立。
因为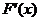 的图象是开口向下的抛物线,
的图象是开口向下的抛物线,
所以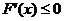 时
时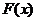 在
在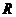 上为减函数,
上为减函数,
所以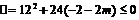 ,解得
,解得 
即 时,
时,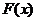 在
在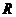 上为减函数。
上为减函数。
20已知函数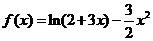 .
.
(1)求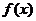 在[0,1]上的单调区间;
在[0,1]上的单调区间;
(2)若对任意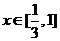 ,不等式
,不等式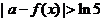 ,求实数a的取值范围.
,求实数a的取值范围.
20解(1)函数f(x)的定义域为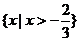 ,
,
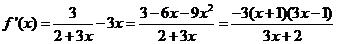
∴在[0,1]上,当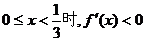 时,
时,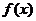 单调递增;
单调递增;
当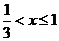 时,
时,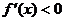 ,
,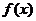 单调递减.
单调递减.
∴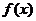 在[0,1]上的增区间是
在[0,1]上的增区间是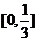 ,减区间是
,减区间是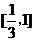 .(开闭均可)
.(开闭均可)
(2)由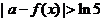 ,可得
,可得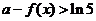 或
或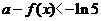 ,
,
即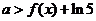 或
或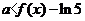 .
.
由(1)当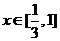 时,
时,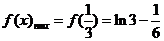 ,
,
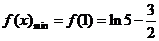 .
.
∵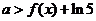 恒成立,∴
恒成立,∴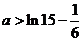 ,
,
∵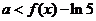 恒成立,∴
恒成立,∴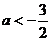 .
.
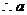 的取值范围为:
的取值范围为: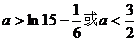
21已知函数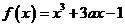 的导函数为
的导函数为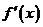 ,
,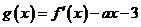 。
。
⑴当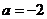 时,求函数
时,求函数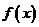 的单调区间;
的单调区间;
⑵若对满足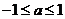 的一切
的一切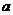 的值,都有
的值,都有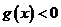 ,求实数
,求实数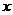 的取值范围;
的取值范围;
⑶若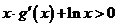 对一切
对一切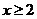 恒成立,求实数
恒成立,求实数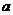 的取值范围。
的取值范围。
21解:⑴当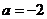 时,
时,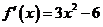 。令
。令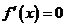 得
得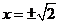 ,故当
,故当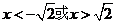 时
时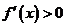 ,
,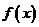 单调递增;当
单调递增;当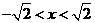 时
时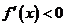 ,
,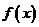 单调递减。所以函数
单调递减。所以函数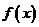 的单调递增区间为
的单调递增区间为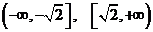 ,单调递减区间为
,单调递减区间为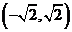 ;
;
⑵法一:因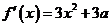 ,故
,故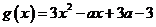 。
。
令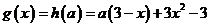 ,要使
,要使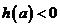 对满足
对满足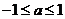 的一切
的一切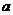 成立,
成立,
则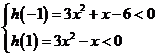 ,解得
,解得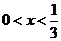 ;
;
法二: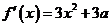 ,故
,故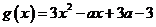 。由
。由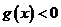 可解得
可解得
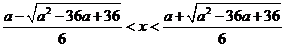 。因为
。因为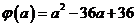 在
在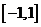 单调递减,因此
单调递减,因此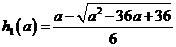 在
在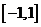 单调递增,故
单调递增,故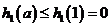 。
。
设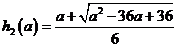 ,则
,则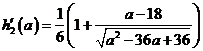 ,
,
因为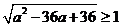 ,所以
,所以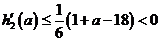 ,从而
,从而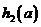 在
在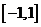 单调递减,
单调递减,
故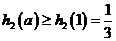 。因此
。因此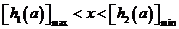 ,即
,即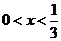 。
。
⑶因为 ,所以
,所以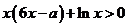 即
即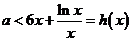 对一切
对一切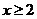 恒成立。
恒成立。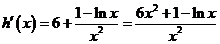 ,令
,令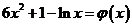 ,则
,则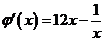 。因为
。因为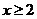 ,所以
,所以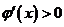 ,故
,故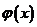 在
在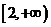 单调递增,有
单调递增,有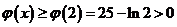 。因此
。因此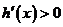 ,从而
,从而 。所以
。所以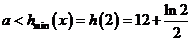 。
。
22设函数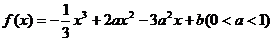 。
。
(1)求函数f(x)的单调区间,并求函数f(x)的极大值和极小值;
(2)当x∈时[a+1,a+2],不等式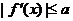 恒成立,求a的取值范围。
恒成立,求a的取值范围。
22解(1)∵f′(x)=-x2+4ax-3a2=-(x-3a)(x-a),由f′(x)>0得:a<x<3a
由f′(x)<0得,x<a或x>3a,
则函数f(x)的单调递增区间为(a,3a),单调递减区间为(-∞,a)和(3a,+∞)列表如下:
|
x |
(-∞,a) |
a |
(a, 3a) |
3a |
(3a,+ ∞) |
|
f′(x) |
- |
0 |
+ |
0 |
- |
|
f(x) |
↘ |
- a3+b a3+b |
↗ |
b |
↘ |
∴函数f(x)的极大值为b,极小值为- a3+b
a3+b
(2)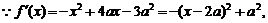
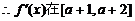 上单调递减,
上单调递减,
因此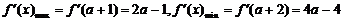
∵不等式|f′(x)|≤a恒成立,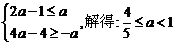
即a的取值范围是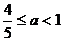
15.若函数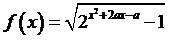 的值域为
的值域为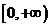 ,则实数
,则实数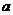 的取值范围是_
的取值范围是_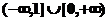 ______。
______。
14.已知曲线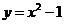 在
在 点处的切线与曲线
点处的切线与曲线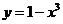 在
在 点处的切线互相平行,则
点处的切线互相平行,则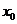 的值为 0或
-2/3
.
的值为 0或
-2/3
.
12.已知函数f(x)=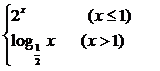 ,则f(1-x)的图象是( D )
,则f(1-x)的图象是( D )
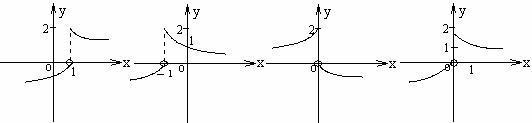
A B C D
二填空题
13已知集合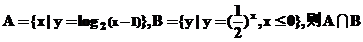 等于
等于 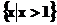
11.若函数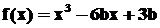 在
在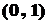 内有极小值,则实数
内有极小值,则实数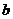 的取值范围是( D )
的取值范围是( D )
A.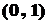 B.
B.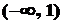 C.
C.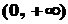 D.
D.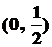
10.函数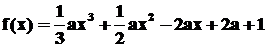 的图象经过四个象限,则实数
的图象经过四个象限,则实数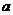 的取值范围是(D )
的取值范围是(D )
A.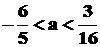 B.
B.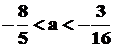 C.
C.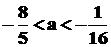 D.
D.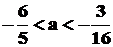
9.设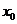 是方程
是方程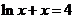 的解,则
的解,则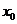 属于区间 ( C )
属于区间 ( C )
A. (0,1) B. (1,2) C. (2,3) D.(3,4)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com