
20. (20)解:(Ⅰ)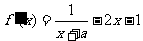 .…………………………………………………2分
.…………………………………………………2分
∵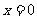 时,
时,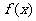 取得极值,∴
取得极值,∴ .…………………………3分
.…………………………3分
故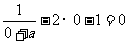 ,解得
,解得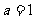 .经检验
.经检验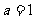 符合题意,∴
符合题意,∴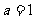 .……………4分
.……………4分
(Ⅱ)由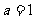 知
知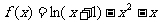 ,由
,由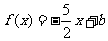 ,得
,得
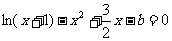 ,令
,令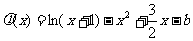 ,则
,则
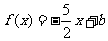 在
在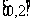 上恰有两个不同的实数根等价于
上恰有两个不同的实数根等价于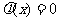 在
在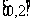 上恰有两个不同实数根.
上恰有两个不同实数根. 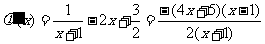 .…………………………6分
.…………………………6分
当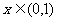 时,
时,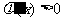 ,于是
,于是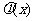 在
在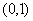 上单调递增;…………7分
上单调递增;…………7分
当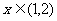 时,
时, ,于是
,于是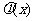 在
在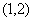 上单调递减.…………8分
上单调递减.…………8分
依题意有 ,…………………………11分
,…………………………11分
解得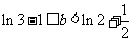 ,∴实数
,∴实数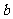 的取值范围是
的取值范围是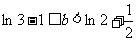 .………12分
.………12分
19. 解:(Ⅰ)证明: 平面
平面 平面
平面 ,
, ,
,
平面 平面
平面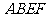 =
=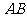 ,
,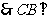 平面
平面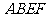 ,
, 平面
平面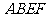 ,
,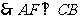 ,又
,又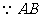 为圆
为圆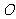 的直径,
的直径,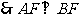 ,
,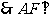 平面
平面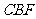 。
。
(Ⅱ)设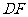 的中点为
的中点为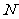 ,则
,则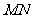
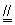
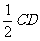 ,又
,又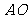
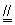
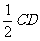 ,则
,则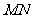
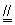
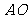 ,
, 为平行四边形,
为平行四边形,
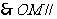
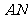 ,又
,又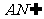 平面
平面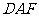 ,
,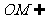 平面
平面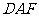 ,
,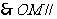 平面
平面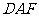 。
。
(Ⅲ)过点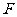 作
作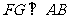 于
于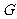 ,
, 平面
平面 平面
平面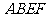 ,
,
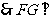 平面
平面 ,
,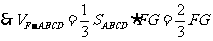 ,
,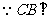 平面
平面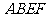 ,
,
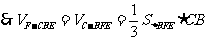
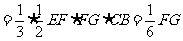 ,
,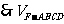
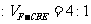 .
.
17.解:
(I)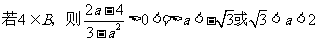 (2分)
(2分)
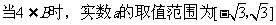 ∪[2,+∞)(4分)
∪[2,+∞)(4分)
(Ⅱ)

(18)解:(Ⅰ)∵随意抽取4件产品检查是随机事件,而第一天有9件正品.
∴第一天通过检查的概率为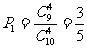 .
.
答:第一天通过检查的概率为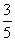 ……………………………4分
……………………………4分
(Ⅱ)第二天通过检查的概率为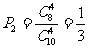 .……………………………6分
.……………………………6分
两天的所得分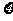 的可取值分别为0,1,2.……………………………7分
的可取值分别为0,1,2.……………………………7分
∵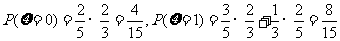 ,
,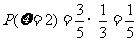 .……10分
.……10分
∴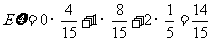 .
.
答:所求的数学期望为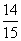 。………………………………12分
。………………………………12分
13. 2 ; 14. 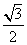 ; 15.
; 15. 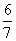 ; 16.
; 16. 
三 解答题(共70分)
22、(本小题满分12分)(请在答题卡上答题)
设函数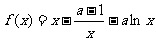
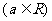 .
.
(I)若 是函数
是函数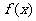 的极大值点,求
的极大值点,求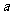 的取值范围;
的取值范围;
(II)当 时,若在
时,若在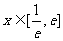 上至少存在一点
上至少存在一点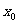 ,使
,使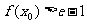 成立,求
成立,求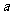 的取值范围.
的取值范围.
 桂林中学高三第二次月考数学试题
桂林中学高三第二次月考数学试题
(理科)答案
一 选择题(每小题5分,共60分)
二 填空题(每小题5分,共20分)
21、(本小题满分12分)(请在答题卡上答题)
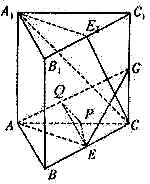
如图,在直三棱柱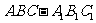 中,
中,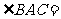 90°,
90°, 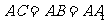 ,
,
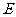 是
是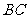 的中点.
的中点.
(Ⅰ)求异面直线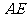 与
与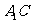 所成的角;
所成的角;
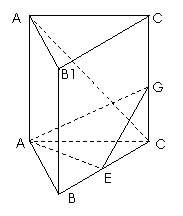 (Ⅱ)若
(Ⅱ)若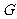 为
为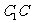 上一点,且
上一点,且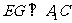 ,求二面角
,求二面角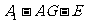 的大小.
的大小.
20、(本小题满分12分)(请在答题卡上答题)
已知函数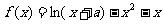 在
在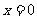 处取得极值.
处取得极值.
(Ⅰ)求实数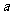 的值;(Ⅱ)若关于
的值;(Ⅱ)若关于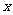 的方程
的方程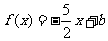 在区间
在区间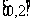 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数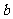 的取值范围.
的取值范围.
19、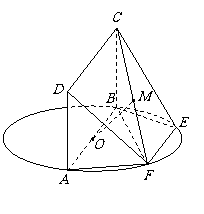 (本小题满分12分)(请在答题卡上答题)
(本小题满分12分)(请在答题卡上答题)
如图, 为圆
为圆 的直径,点
的直径,点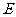 、
、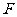 在圆
在圆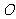 上,
上,
 ,矩形
,矩形 所在的平面和圆
所在的平面和圆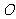 所在的平面
所在的平面
互相垂直,且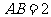 ,
,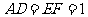 .
.
(Ⅰ)求证: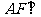 平面
平面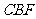 ;
;
(Ⅱ)设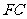 的中点为
的中点为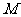 ,求证:
,求证: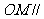 平面
平面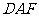 ;
;
(Ⅲ)设平面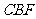 将几何体
将几何体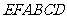 分成的
分成的
两个锥体的体积分别为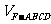 ,
,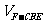 ,求
,求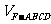
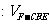 .
.
18、(本小题满分12分)(请在答题卡上答题)
某车间在两天内,每天生产10件某产品,其中第一天、第二天分别生产出了1件、2件次品.而质检部门每天要从生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(Ⅰ)求第一天产品通过检查的概率;
(Ⅱ)若厂内对车间生产的产品采用记分制:两天全不通过检查得0分;通过1天、2天分别得1分、2分.求该车间这两天的所得分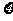 的数学期望.
的数学期望.
17、(本小题满分10分)(请在答题卡上答题)
已知集合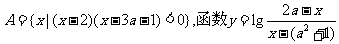 的定义域为集合B,
的定义域为集合B,
(I)若4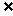 B,求实数a的取值范围;(Ⅱ)求使B
B,求实数a的取值范围;(Ⅱ)求使B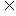 A的实数a的取值范围
A的实数a的取值范围
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com