
5.已知数列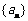 中,
中,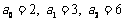 ,且对
,且对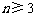 时,有
时,有
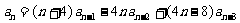 .
.
(Ⅰ)设数列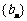 满足
满足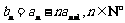 ,证明数列
,证明数列 为等比数列,并求数列
为等比数列,并求数列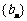 的通项公式;
的通项公式;
(Ⅱ)记 ,求数列
,求数列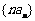 的前n项和Sn.
的前n项和Sn.
4.在数列{an}中,a1=1,an+1=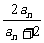 (n∈N*),则
(n∈N*),则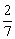 是这个数列的第_________项.
是这个数列的第_________项.
1. 等差数列{an}中,Sn是其前n项和,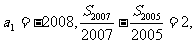 则S2008的值为
则S2008的值为
2:已知等比数列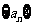 中
中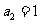 ,则其前三项的和
,则其前三项的和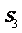 的取值范围是
的取值范围是
3:定义“等积数列”:在一个数列中,如果每一项与它的后一项的积都为同一常数,那么这个数列叫做已知数列,这个常数叫该数列的公鸡积,已知数列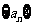 I等级数列,且
I等级数列,且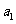 =2,公积为5,
=2,公积为5,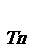 为数列
为数列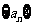 的前n项和,则
的前n项和,则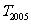 =
=
8. 解:由数列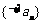 中各项均为1,知数列
中各项均为1,知数列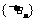 是首项为
是首项为 ,公差为1的等差数列,所以,
,公差为1的等差数列,所以,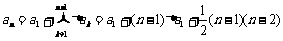 .这说明,
.这说明,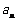 是关于
是关于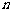 的二次函数,且二次项系数为
的二次函数,且二次项系数为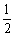 ,由
,由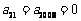 ,得
,得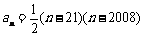 ,从而
,从而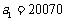 .
.
点评:等差比数列的通项公式和前n项和的公式是数列中的基础知识,必须牢固掌握.
三 范例剖析
例1 数列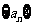 的前
的前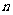 项和记为
项和记为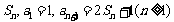 .
.
(Ⅰ)求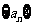 的通项公式;
的通项公式;
(Ⅱ)等差数列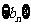 的各项为正,其前
的各项为正,其前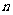 项和为
项和为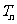 ,且
,且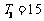 ,又
,又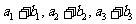 成等比数列,求
成等比数列,求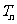 .
.
辨析:已知数列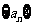 的前三项与数列
的前三项与数列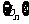 的前三项对应相同,且
的前三项对应相同,且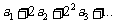
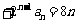 对任意的
对任意的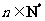 都成立,数列
都成立,数列 是等差数列.
是等差数列.
⑴求数列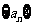 与
与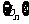 的通项公式;
的通项公式;
⑵是否存在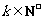 ,使得
,使得 ,请说明理由.
,请说明理由.
例2 已知各项均为正数的数列{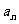 }满足
}满足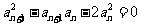 (
(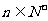 ),且
),且 是
是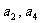 的等差中项.
的等差中项.
(Ⅰ)求数列{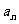 }的通项公式
}的通项公式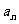 ;
;
(Ⅱ)若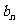 =
=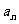
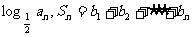 ,求使S
,求使S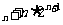 >50成立的正整数n的
>50成立的正整数n的
最小值.
变式: 已知递增的等比数列{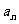 }满足
}满足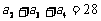 ,且
,且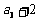 是
是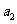 ,
,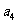 的等差中项.
的等差中项.
(1)
求{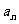 }的通项公式
}的通项公式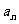 ;
;
(2) 若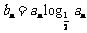 ,
,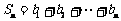 求使
求使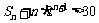 成立的
成立的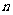 的最小值.
的最小值.
例3 数列{an}中,a1=8,a4=2,且满足:an+2-2an+1+an=0(n∈N*),
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设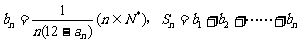 ,是否存在最大的整数m,使得任意的n均有
,是否存在最大的整数m,使得任意的n均有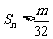 总成立?若存在,求出m;若不存在,请说明理由.
总成立?若存在,求出m;若不存在,请说明理由.
辨析:已知数列{an}的前n项为和Sn,点(n,)在直线y= x+上.数列{bn}满足 bn+2-2bn+1+bn=0(nÎN*),且b3=11,前9项和为153.
(1)求数列{an},{bn}的通项公式;
(2)设cn= ,数列{cn}的前n项和为Tn,求使不等式Tn>对一切nÎN*都成立的最大正整数k的值;
(3)设nÎN*,f(n)= 问是否存在mÎN*,使得f(m+15)=5f(m)成立?若存在,求出m的值;若不存在,请说明理由.
四 巩固训练
7.解: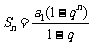 ,
,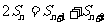 ,则有
,则有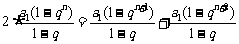 ,
,
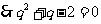 ,
,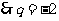 .,
., 时,
时,
6.解: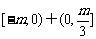 . 解:设
. 解:设 ,则有
,则有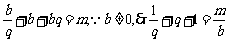 .
.
当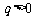 时,
时,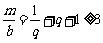 ,而
,而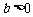 ,
,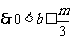 ;当
;当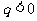 时,
时,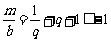 ,即
,即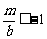 ,而
,而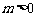 ,
,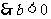 ,则
,则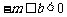 ,故
,故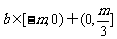
4. 解:84 5. 解:.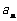 =
=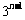 .
.
3.解:解法1:“若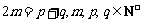 ,则
,则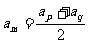 ”解析:
”解析: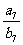 =
=
解法2: 可设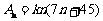 ,
,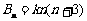 ,则
,则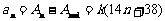 ,
, 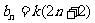 ,则
,则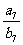 =
=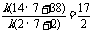
2.解:依题意,中间项为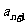 ,于是有
,于是有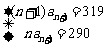 解得
解得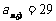 .1分析:本题主要是考查等比数列的基本概念和性质,可利用方程思想将等比数列问题转化为
.1分析:本题主要是考查等比数列的基本概念和性质,可利用方程思想将等比数列问题转化为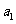 和
和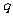 处理,也可利用等比数列的定义进行求解.设公比为
处理,也可利用等比数列的定义进行求解.设公比为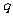 ,由题知,
,由题知,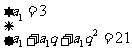 得
得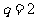 或
或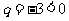 (舍去),∴
(舍去),∴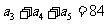
1.解:利用等差数列的性质得: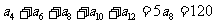 ,
,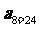 ,
,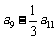 =
=
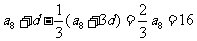
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com