12.(13分)甲、乙两运动员在训练交接棒的过程中发现：甲经短距离加速后能保持以9 m/s的速度跑完全程；乙从起跑后到接棒前的运动是匀加速的.为了确定乙起跑的时机，需在接力区前适当的位置设置标记.在某次练习中，甲在接力区前s0＝13.5 m 处作了标记，并以v＝9 m/s的速度跑到此标记时向乙发出起跑口令.乙在接力区的前端听到口令时起跑，并恰好在速度达到与甲相同时被甲追上，完成交接棒.已知接力区的长度L＝20 m.求：

(1)此次练习中乙在接棒前的加速度a的大小.

(2)在完成交接棒时乙离接力区末端的距离.[2007年高考·全国理综卷Ⅰ]

解析：(1)设经过时间t，甲追上乙，则根据题意有：

vt－＝13.5 m

将v＝9 m/s代入，得：t＝3 s

再由v＝at，解得：a＝3 m/s2.

(2)甲追上乙时，设乙跑过的距离为s，则：

s＝at2

代入数据得：s＝13.5 m

所以乙离接力区末端的距离为：

Δs＝20 m－13.5 m＝6.5 m.

答案：(1)3 m/s2　(2)6.5 m

11.(13分)摩托车先由静止开始以 m/s2的加速度做匀加速运动，后以最大行驶速度25 m/s匀速运动，追赶前方以15 m/s的速度同向匀速行驶的卡车.已知摩托车开始运动时与卡车的距离为1000 m，则：

(1)追上卡车前，二者相隔的最大距离是多少？

(2)摩托车经过多长时间才能追上卡车？

解析：(1)由题意得，摩托车匀加速运动的最长时间t1＝＝16 s，位移s1＝＝200 m＜s0＝1000 m，所以摩托车在达到最大速度之前没有追上卡车.则追上卡车前二者速度相等时，间距最大，设从开始经过t2时间速度相等，最大间距为sm，于是有at2＝v匀，所以t2＝＝9.6 s

最大间距sm＝s0+v匀t2－at＝1072 m.

(2)设从开始经过t时间摩托车追上卡车，则有：

+vm(t－t1)＝s0+v匀t

解得：t＝120 s.

答案：(1)1072 m　(2)120 s

10.现有一根长2 m左右的细线、5个铁垫圈和一个金属盘.在线的下端系上第一个垫圈，隔12 cm再系一个，以后垫圈之间的距离分别为36 cm、60 cm、84 cm，如图所示.站在椅子上，向上提起线的上端，让线自由垂下，且第一个垫圈紧靠放在地上的金属盘.松手后开始计时，若不计空气阻力，取g＝10 m/s2，则第2、3、4、5各垫圈(　)

A.落到盘上的声音时间间隔越来越大

B.落到盘上的声音时间间隔相等

C.依次落到盘上的速率比为1∶∶∶2

D.依次落到盘上的时间比为1∶(－1)∶(－)∶(2－)

解析：由h＝gt2得，时间间隔t1＝ s＝2 s，t2＝－t1＝2 s，t3＝－t2＝2 s……由此可见时间间隔相等.

落到盘上的速度v1＝ m/s＝2 m/s，v2＝ m/s＝4 m/s，

v3＝ m/s＝6 m/s……

可得v1∶v2∶v3∶…∶vn＝1∶2∶3∶…∶n.

答案：B

非选择题部分共3小题，共40分.

9.如图甲所示，两个光滑的斜面高度相同，右边由两部分组成，且AB+BC＝AD.两小球a、b分别从A点沿两侧斜面由静止滑下，不计转折处的能量损失，两次下滑的时间分别为t1与t2，则(　)

A.t1＞t2　　　　B.t1＜t2

C.t1＝t2　 D.无法判断

解析：由于在下滑的过程中不损失机械能，因此质点到达C点和D点的速度大小均为v，如图乙所示，即两次下滑的速率随时间变化的v－t图象中图线的终点均应落在直线vF上.OF为沿AD下滑的v－t图线，OG为下滑AB段的图线，由于AB段的加速度比AD段的大，故OG的斜率比OF的斜率大.GH为BC段图线，H落在vF上，那么H落在F的左边、右边还是与F重合呢？

若H正好与F重合，那么四边形OGHt1的面积比三角形OFt1的面积大，这说明沿ABC下滑的路程较大，这与AD＝AB+BC相矛盾，所以H不可能与F重合，即t1不可能等于t2.

若H在F的右边，如图丙所示.过H作HI∥OF交t轴于I，则S△HIt2＝S△FOt1，而△HIt2是四边形OGHt2的一部分，故S四边形OGHt2＞S△FOt1，与题设矛盾，所以H只能在F的左边，即t1＞t2.选项A正确.

答案：A

8.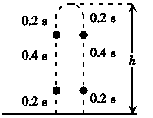一杂技演员用一只手抛球、接球.他每隔0.40 s抛出一球，接到球便立即把球抛出.已知除抛、接球的时刻外，空中总有四个球.将球的运动近似看做是竖直方向的运动，则球到达的最大高度是(高度从抛球点算起，取g＝10 m/s2)(　)

A.1.6 m　　B.2.4 m　　C.3.2 m　　D.4.0 m

解析：根据题意可得4个球可能处于如图所示的状态，则：

h＝gt2＝×10×(0.8)2 m＝3.2 m，故选项C正确.

答案：C

7.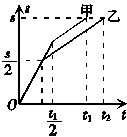甲、乙两车同时同向沿直线驶向某地，甲在前一半时间内以v1的速度匀速运动，后一半时间内以v2的速度匀速运动，v1≠v2；而乙车在前一半路程内以v1做匀速运动，后一半路程内以v2做匀速运动.两车运动的总时间分别为t1、t2，则可判定(　)

A.t1＝t2

B.t1＜t2

C.t1＞t2

D.无法确定t1、t2的大小关系

解析：

解法一　这道题用s－t图象进行分析比较简单，题中没有交代v1和v2的大小关系，我们可假设v1＞v2，则前半段的s－t图线的倾斜度大，后半段的s－t图线的倾斜度小.画出甲、乙两车运动的s－t图象，从图中不难看出，甲车先到达目的地.如果假设v2＞v1，也可得到同样的结论.

解法二　甲车以较大的速度行驶的位移一定大于，故甲车先到达目的地.

答案：B

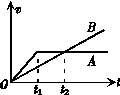
6.图示是两个由同一地点出发、沿同一直线向同一方向运动的物体A和B的速度图象.运动过程中A、B的情况是(　)

A.A的速度一直比B的大，B没有追上A

B.B的速度一直比A的大，B追上A

C.A在t1时刻后改做匀速直线运动，在t2时刻B追上A

D.在t2时刻A、B的瞬时速度相等，A在B的前面，尚未被B追上，但此后总是要被追上的

解析：0-t2时间内vA＞vB；t＞t2时，vB＞vA，故选项A、B、C错误.当t＞t2时，vB＞vA，B将追上A，选项D正确.

答案：D

5.一质点的位移s与时间t的关系如图甲所示，能正确表示该质点的速度v与时间t的关系的图象是图乙中的(　)

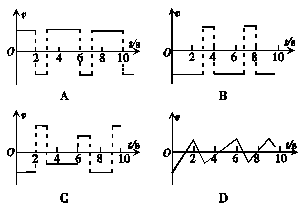
乙

解析：由s－t图象可知，在0-2 s内质点做匀速直线运动，速度为负；在2-3 s内质点做匀速直线运动，速度为正，且大于0-2 s内的速度……故选项C正确.

答案：C

4.设物体运动的加速度为a、速度为v、位移为s.现有四个不同物体的运动图象如图所示，假设物体在t＝0时的速度均为零，则其中表示物体做单向直线运动的图象是(　)

解析：A图可直接看出位移有正负变化；表示做往复运动；B图可直接看出速度有正负变化，由v＝v0+at可得D图表示的物体的v－t图象为B图；而C图表示的v－t图象如下图所示，即为单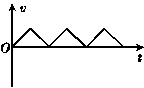向直线运动.

答案：C

甲

3.一个从地面竖直上抛的物体两次经过一个较低点A的时间间隔是5 s，两次经过一个较高点B的时间间隔是3 s，则A、B之间的距离是(取g＝10 m/s2)(　)

A.80 m　　　　B.40 m

C.20 m　 D.初速度未知，无法确定

解析：由竖直上抛运动的特性可知，B点离最高点的距离hB＝×10×()2 m＝11.25 m

A点离最高点的距离hA＝×10×()2 m＝31.25 m

故sAB＝20 m.

答案：C