
2.(2009·山东淄博模拟)自2007年6月29日以来,淮河上游及安徽省合肥市以北部分地区普降大到暴雨,致使淮河干支流水位迅猛上涨,同时,安徽沿淮、淮北地区内涝严重,淮河抗灾救灾形势十分严峻,这是继2003年以来淮河发生的又一次全流域性洪水。据相关知识,回答下列问题。

(1)试分析造成此次淮河流域洪涝灾害的主要原因。
(2)利用“淮河流域图”中有关信息,从以下几方面分析淮河流域洪涝灾害易发的原因。
①从地理位置、气候方面分析 。
②从流域地形特点、水系方面分析 。
③该河没有天然入海口,入海水道主要有两条通道,一条是向东通过苏北灌溉总渠,注入 海;一条是向南借道 (河流),再流入海洋。
④从人地关系角度分析 。
(3)治理淮河流域的洪涝灾害,你有什么措施?
(4)在洪水危险区和多发区的个人和家庭,应如何做好防洪准备?
答案 (1)淮河流域洪涝灾害产生原因主要是:影响我国的锋面雨带在该地区停留时间较长(或受准静止锋的影响),导致降水量大,造成洪涝灾害的发生。
(2)①淮河流域地处我国南北过渡地带,其降水兼有北方地区的暴雨集中、降水量变化大和南方地区的暴雨历时长、强度大的特点,易造成水灾
②地形:淮河流域地势是两头翘,中游地势较低,而下游因为黄河改道淤积,地势较高,排水不畅,没有天然的入海口。水系:北岸支流长而多,水流缓;南岸支流短,水流急,积水快
③黄 长江
④淮河流域开发历史久,人口众多,人地关系矛盾突出,毁林开荒导致水土流失严重,加之黄河改道致使下游河床、湖泊淤积严重,水流不畅,洪灾多发
(3)非工程措施:植树造林,建立防护林体系,保持水土。
工程措施:上游修水库,中游建设蓄洪、分洪工程,下游挖入海新河。
(4)关注汛期天气预报;学习并具备游泳、划船等技能;准备逃生物资等。
1.气候及其异常变化往往成为许多自然灾害的致灾因子。读“我国四地气候资料统计图”,回答问题。
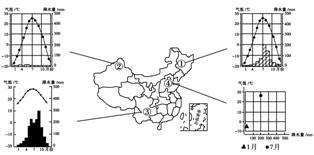
(1)①地霜冻灾害比②、④地频繁,试简析原因。
(2)②地气候干旱,降水稀少,但局部地区仍时有洪水发生,其原因是什么?
(3)③地是我国滑坡、泥石流灾害的多发地区,与这里的哪些气候特点有关?
(4)危害④地农业生产最严重的生物灾害是什么,原因有哪些?
答案 (1)①地与②地相比,气候湿润,是我国重要的农业区,农作物播种面积大。
①地与④地区相比,纬度更高,更靠近冬季风源地,降温强度更大,初霜开始更早,终霜结束更晚。
(2)受气温升高影响,4-5月(春季)形成融雪洪水;7-8月(夏季)形成融冰洪水。
(3)这里是亚热带季风气候,夏季降水集中,多暴雨。
(4)蝗灾。这里的降水时间变化大,干旱少雨年份或者旱季,河湖退水区适宜雌蝗产卵;雨季多雨利于蝗虫幼虫生长。
22. (本题满分12分)若函数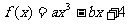 ,当
,当 时,函数
时,函数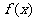 有极值
有极值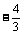 ,
,
(1)求函数的解析式;
(2)若函数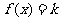 有3个解,求实数
有3个解,求实数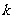 的取值范围.
的取值范围.
解: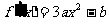 ………………2分
………………2分
(1)由题意: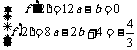 ………4分 解得
………4分 解得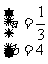 …………6分
…………6分
 所求解析式为
所求解析式为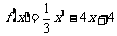
(2)由(1)可得: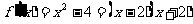
令 ,得
,得 或
或 ………………………………8分
………………………………8分
当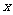 变化时,
变化时, 、
、 的变化情况如下表:
的变化情况如下表:
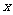 |
 |
 |
 |
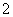 |
 |
 |
 |
 |
- |
 |
 |
 |
单调递增↗ |
 |
单调递减↘ |
 |
单调递增↗ |
 因此,当
因此,当 时,
时, 有极大值
有极大值 …………………9分
…………………9分
当 时,
时, 有极小值
有极小值 …………………10分
…………………10分
 函数
函数 的图象大致如图:……13分
y=k
的图象大致如图:……13分
y=k
由图可知: ………………………14分
………………………14分
21. (本题满分12分) 某工厂拟建一座平面图(如图所示)为矩形且面积为200m2 的三级污水处理池,由于地形限制,长、宽都不能超过16m.如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).(1)写出总造价y(元)与污水处理池长x(m)的函数关系式,并指出其定义域;
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求出最低总造价.
解:①因污水处理水池的长为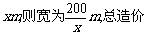
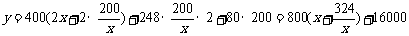 .由题设条件
.由题设条件 即函数定义域为[12.5,16]
即函数定义域为[12.5,16]
②先研究函数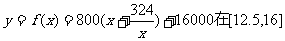 上的单调性,
上的单调性,
对于任意的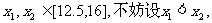
则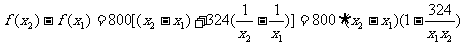
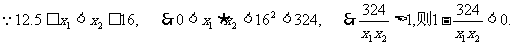
又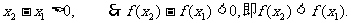
故函数y=f(x)在[12.5,16]上是减函数. ∴当x=16时,y取得最小值,此时
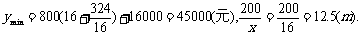
综上,当污水处理池的长为16m,宽为12.5m时,总造价最低,最低为45000元.
19. (本题满分12分)已知函数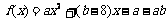
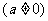 ,当
,当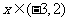 时,
时,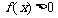 ;当
;当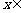 (
( )
)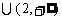 时,
时,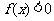 .(1)求
.(1)求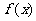 在[0,1]内的值域;(2)
在[0,1]内的值域;(2)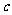 为何值时,不等式
为何值时,不等式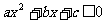 在[1,4]上恒成立.
在[1,4]上恒成立.
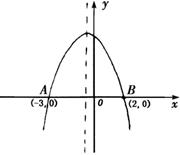 解:由题意得
解:由题意得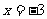 和
和 是函数
是函数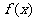 的零点且
的零点且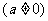 ,则
,则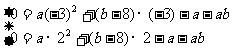 (此处也可用韦达定理解)解得:
(此处也可用韦达定理解)解得: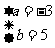
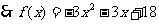 ---6分
---6分
(1)由图像知,函数在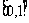 内为单调递减,所以:当
内为单调递减,所以:当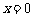 时,
时,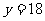 ,当
,当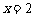 时,
时,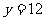 .
.
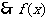 在
在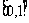 内的值域为
内的值域为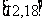 --------- 8分
--------- 8分
(2)令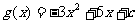 因为
因为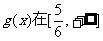 上单调递减,要使
上单调递减,要使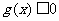 在[1,4]上恒成立,则需要
在[1,4]上恒成立,则需要 ,即
,即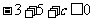
解得
 当
当 时,不等式
时,不等式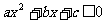 在[1,4]上恒成立. ------12分
在[1,4]上恒成立. ------12分
 20. (本题满分12分)已知函数
20. (本题满分12分)已知函数 (
(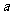 为实常数).(1)若
为实常数).(1)若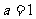 ,作函数
,作函数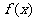 的图像;(2)当a>
的图像;(2)当a>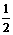 时,
时,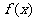 在区间
在区间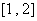 上的最小值为
上的最小值为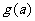 ,求
,求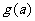 的表达式。
的表达式。
解:(1)当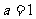 时,
时,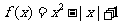
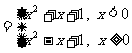 .作图 ……(6分)
.作图 ……(6分)
(2)当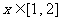 时,
时,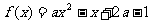 .
.
若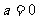 ,则
,则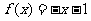 在区间
在区间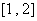 上是减函数,
上是减函数,
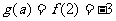 .……(5分)
.……(5分)
若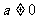 ,则
,则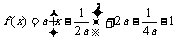 ,
,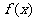 图像的对称轴是直线
图像的对称轴是直线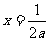 .
.
当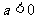 时,
时,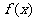 在区间
在区间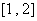 上是减函数,
上是减函数,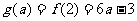 .……(6分)
.……(6分)
当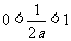 ,即
,即 时,
时,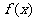 在区间
在区间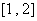 上是增函数,
上是增函数,
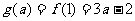 .……(7分)
.……(7分)
当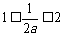 ,即
,即 时,
时,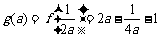 ,……(8分)
,……(8分)
当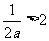 ,即
,即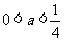 时,
时,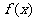 在区间
在区间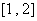 上是减函数,
上是减函数,
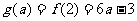 .……(9分)
.……(9分)
综上可得
 .……(10分)
.……(10分)
18.(本题满分12分)已知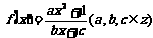 是奇函数,又
是奇函数,又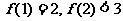 ,求
,求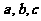 的值.
的值.
∵f(x)为奇函数,∴f(-x)=-f(x), ……………….1分
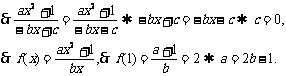 ………………………5分
………………………5分
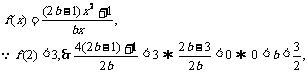 ……………………10分
……………………10分
∵a,b, c, ∈Z ,∴b=1, ∴a=1, 综上 ,a=1, b=1, c=0……………………12分
17. (本题满分10分)若集合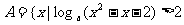 ,
, 且
且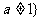 .(1)若
.(1)若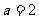 ,求集合
,求集合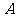 ; (2)若
; (2)若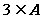 ,求
,求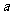 的取值范围.
的取值范围.
[解](1)若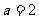 ,
,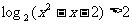 ,则
,则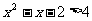 ………………2分
………………2分
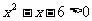 ,
, ,得
,得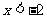 或
或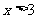 ………………4分
………………4分
所以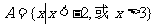 ………………5分
………………5分
(2)因为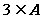 ,所以
,所以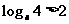 ………………6分
………………6分
, 所以 a>1 ………… ……8分
且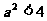 所以
所以 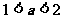 ………………10分
………………10分
16. 已知偶函数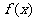 在区间
在区间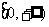 单调增加,则满足
单调增加,则满足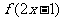 <
<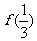 的x 取值范围是________________________
的x 取值范围是________________________
[解析]由于f(x)是偶函数,故f(x)=f(|x|)∴得f(|2x-1|)<f(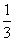 ),再根据f(x)的单调性
),再根据f(x)的单调性
得|2x-1|<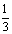 解得
解得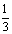 <x<
<x<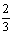
15. 定义在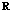 上的函数
上的函数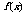 满足
满足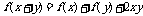 (
(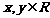 ),
),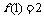 ,则
,则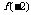 =_____2
=_____2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com