1、利用离散型随机变量的方差与期望的知识，可以解决实际问题。利用所学知识分析和解决实际问题的题型，越来越成为高考的热点，应予重视。

例1、(1)下面说法中正确的是　　　　　　　　　　　　　　　　　 (　)

A．离散型随机变量ξ的期望Eξ反映了ξ取值的概率的平均值。

B．离散型随机变量ξ的方差Dξ反映了ξ取值的平均水平。

C．离散型随机变量ξ的期望Eξ反映了ξ取值的平均水平。

D．离散型随机变量ξ的方差Dξ反映了ξ取值的概率的平均值。

解：选C

说明：此题考查离散型随机变量ξ的期望、方差的概念。

(2)、(2001年高考题)一个袋子里装有大小相同的3个红球和2个黄球，从中同时取出两个，则其中含红球个数的数学期望是　　　　 。

解：含红球个数ξ的Eξ=0× +1× +2× =1.2

说明：近两年的高考试题与《考试说明》中的“了解……，会……”的要求一致，此部分以重点知识的基本题型和内容为主，突出应用性和实践性及综合性。考生往往会因对题意理解错误，或对概念、公式、性质应用错误等，导致解题错误。

例2、设 是一个离散型随机变量，其分布列如下表，试求E 、D

　剖析：应先按分布列的性质，求出 的值后，再计算出E 、D 。

解：因为随机变量的概率非负且随机变量取遍所有可能值时相应的概率之和等于1，所以 解得 。

于是， 的分布列为

所以E ＝(－1) ，

D ＝

说明：解答本题时，应防止机械地套用期望和方差的计算公式，出现以下误解：E ＝ 。

练习：已知ξ的分布列为

(1)求Eξ,　Dξ,　δξ，

(2) 若η=2ξ+3,求Eη,Dη

解：(1)Eξ= ,　Dξ ,

δξ=

(2)Eη=E(2ξ+3)= 2 Eξ+3= ,　　　Dη=

例3、人寿保险中(某一年龄段)，在一年的保险期内，每个被保险人需交纳保险费 元，被保险人意外死亡则保险公司赔付3万元，出现非意外死亡则赔付1万元，经统计此年龄段一年内意外死亡的概率是 ，非意外死亡的概率为 ，则 需满足什么条件，保险公司才可能盈利？

剖析：要使保险公司能盈利，需盈利数 的期望值大于0，故需求E 。

解：设 为盈利数，其概率分布为

且E ＝

要盈利，至少需使 的数学期望大于0，故 。

说明：(1)离散型随机变量的期望表征了随机变量取值的平均值

(2)本题中D 有什么实际意义？

例4：把4个球随机地投入4个盒子中去，设 表示空盒子的个数，求E 、D

剖析：每个球投入到每个盒子的可能性是相等的，总的投球方法数为 ，空盒子的个数可能为0个，此时投球方法数为 ；空盒子的个数为1时，此时投球方法数为 ， 。

解： 的所有可能取值为0，1，2，3。

。

　所以 的分布列为：

所以E ＝ ，D ＝ 。

说明：本题的关键是正确理解 的意义，写出 的分布列。

例5、已知两家工厂，一年四个季度上缴利税如下：(单位：万元)

试分析两厂上缴利税状况，并予以说明。

解：设随机变量ξ与η分别表示甲、乙两厂上缴利税数，

依题意有P(ξ=k)= ，P(η=k)= (k=1，2，3，4)

Eξ= ×(70+50+80+40)=60

Eη= ×(55+65+55+65)=60

Eξ²= ×(70²+50²+80²+40²)=3850

Eη²= ×(55²+65²+55²+65²)=3625

Dξ=Eξ²-(Eξ)²=250，Dη=Eη²-( Eη)²=25

由上述计算可知，两厂上缴利税的期望相等，说明平均水平相同；而甲厂的方差大于乙厂的方差，说明乙厂的波动性小，生产稳定；甲厂的波动性大，导致生产不稳定。

说明：本题考查利用离散型随机变量的方差与期望的知识，分析解决实际问题的能力。

例6、(1)设随机变量ξ具有分布列为P(ξ=k)= (k=1，2，3，4，5，6)，

求Eξ、E(2ξ+3)和Dξ。

(2) 设随机变量ξ的分布列为P(ξ=k)= 　(k=1，2，3，…，n)，求Eξ和Dξ。

(3)一次英语测验由50道选择题构成，每道有4个选项，其中有且仅有一个是正确的，每个选对得3分，选错或不选均不得分，满分150分，某学生选对每一道题的概率为0.7，求该生在这次测验中的成绩的期望与方差。

解：(1)Eξ=x₁P₁+x₂P₂+x₃P₃+…+x₆P₆=1× +2× +3× +…+6× =3.5

E(2ξ+3)=2Eξ+3=10

Dξ=(x₁-Eξ)²P₁+(x₂-Eξ)²P₂+…+(x₆-Eξ)²P₆

= [(1-3.5)²+(2-3.5)²+…(6-3.5)²]=17.5×

(2) Eξ= (1+2+…+n)=

Dξ=Eξ²-(Eξ)²= (n²-1)

(3)设ξ为该生选对试题个数，η为成绩。则ξ-β(50，0.7)，η=3ξ

∴Eξ=50×0.7=35；Dξ=50×0.7×0.3=10.5

故Eη=E(3ξ)=3Eξ=105

Dη=D(3ξ)=9Dξ=94.5

说明：可根据离散型随机变量的期望和方差的概念、公式及性质解答。

3、特别注意：在计算离散型随机变量的期望和方差时，首先要搞清其分布特征及分布列，然后要准确应用公式，特别是充分利用性质解题，能避免繁琐的运算过程，提高运算速度和准确度。

2、 方差、标准差定义：

Dξ=(x₁-Eξ)²·P₁+(x₂-Eξ)²·P₂+…+(x_n-Eξ)²·P_n+…称为随机变量ξ的方差。

Dξ的算术平方根 =δξ叫做随机变量的标准差。

随机变量的方差与标准差都反映了:随机变量取值的稳定与波动、集中与离散的程度。

且有D(aξ+b)=a²Dξ,可以证明Dξ=Eξ²- (Eξ)²。

若ξ-B(n，p)，则Dξ=npq，其中q=1-p.

1、 期望的定义：

一般地，若离散型随机变量ξ的分布列为

则称Eξ=x₁P₁+x₂P₂+x₃P₃+…+x_nP_n+…为ξ的数学期望或平均数、均值，简称期望。

它反映了:离散型随机变量取值的平均水平。

若η=aξ+b(a、b为常数)，则η也是随机变量，且Eη=aEξ+b。　 E(c)= c

特别地，若ξ- B(n，P)，则Eξ=nP

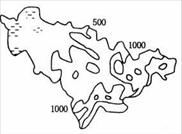读东北某省地形示意图，完成28-30题。

28．有关该省的叙述正确的是

A．地势西北高，东南低

B．降水东南多，西北少

C．山地丘陵多，平原少，地块小

D．平原地区春旱严重，不利农业生产

29．分布在该省的平原及主要经济作物分别是

A．三江平原　 甜菜　 B．辽河平原　 大豆　 C．松嫩平原　 玉米　 D．松嫩平原　 亚麻

30．有关该省东南部地区的叙述，正确的是

A．为西北--东南走向的山地　　　　　 B．天然植被为亚寒带针叶林

C．可采集到名贵药材　　　　　　　　　 D．该地河流含沙量高，结冰期短

长春外国语学校

2009----2010学年第一学期期中考试高二年级

27．关于东北地区内部不同区域农业发展方向的叙述，正确的是

A．平原区面向国内大宗农产品需求市场，继续强化商品粮、豆等大宗农产品市场

B．平原区的发展方向是加快发展农产品加工业，促进粮食转化，延长产业链

C．西部草原区的发展方向是多元开发特色农产品，在半山区实现“立体开发”

D．山区农业发展方向是大力发展生态农业和舍饲畜牧业

26．东北地区成为我国重要的商品粮基地的主要原因是

A．耕地面积广大，适宜大规模机械化耕作 B．宜农荒地多

C．土壤肥沃　　　　　　　　　　　　　 D．人少地多，人均耕地全国最多

25．针对东北地区的土地、森林、气候资源等自然条件和良好的工业基础、便利的交通条件，东北地区将建成全国性的：①商品粮基地　 ②商品棉基地　 ③林业基地　

④畜牧业基地

A．①②　　　　　　 B．②③　　　　　　 C．①②③　　　　　 D．①③④

流域的开发以河流的利用与治理为核心，结合流域的具体特征，对资源进行综合开发和利用。据此完成23-24题。

23．TVA主要负责田纳西河流域的统一开发和管理。它所确定的流域开发的核心是

A．河流的梯级开发　　　　　　　　　　　 B．流域的综合开发

C．流域生态环境的恢复的治理　　　　　　 D．防洪

24．TVA在流域过程中，合理利用土地的主要措施是：①留出土地用于生态恢复和建立自然保护区 ②调整农、林、牧业结构 ③恢复治理采矿区的土地生态 ④建立公园、野生动物管理区、风景区

A．①②③　 　　　　B．②③④　　　　　 C．①②④　 　　　　D．①③④