6.解：依题意，所以

7解：锐角三角形。由题意得，

　是锐角三角形．

8.如图甲是第七届国际数学教育大会(简称ICME－7)的会徽图案，会徽的主体图案是由如图乙的一连串直角三角形演化而成的，其中，如果把图乙中的直角三角形继续作下去，记的长度构成数列，则此数列的通项公式为＝　 　　．

二　感悟解答

1解：=2=6，=3，5=15，答：15

2解：的奇偶性为：奇，奇，偶，偶，奇，奇，偶，偶，…，从而分别为： ，，1，1，，，1，1，…，周期为4，所以，．答： 2

3解：换底公式：．为整数，，m∈N*分别是，最大值≤2008，m最大可取10，故和为2²+2³+…+2¹⁰-18=2026．

4解：． 是偶函数，是奇，

，是等比数列 ，．

5解： 11,12,13,14,15．解: 圆心,半径

故与PC垂直的弦是最短弦，所以而过P、C的弦是最长弦，所以

由等差数列，

7．在△ABC中，是以－4为第3项，4为第7项的等差数列的公差，是以为第3项，9为第6项的等比数列的公比，则这个三角形是　　　　　 ．

6．(08湖北卷理14)已知函数,等差数列的公差为.若

,则　　　　　　 .

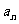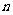5．在圆内，过点有条弦，它们的长构成等差数列，若为过该点最短弦的长,为过该点最长弦的长,公差，那么的值是　　　　　 ．

4．已知函数是偶函数，是奇函数，正数数列满足，，求数列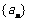的通项公式为　　　　 ．

3. 给定(n∈N*)，定义乘积为整数的k(k∈N*)叫做“理想数”，则区间[1，2008]内的所有理想数的和为　　 　　　　．

2. 在数列中，，，在数列中，，，则_________．

1．在等差数列{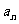}中，则　 ．

22．(本小题满分14分)

　已知函数(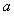为常数)是R上的奇函数，函数g(x)=是区间上的减函数.

(Ⅰ)求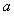的值；

(Ⅱ)若上恒成立，求t的取值范围；

(Ⅲ)讨论关于x的方程的根的个数．

潍坊七中2009-2010学年第一学期第一学段学分认定模块考试