
试卷包含选择题、填空题和解答题三种题型。其中选择题是四选一型的单项选择题;填空题只要求直接写出结果,不必写出计算过程或推证过程;解答题包括计算题、证明题和应用题等。解答应写出文字说明、演算步骤或推理论证过程。三种题型所占分数的百分比约为:选择题占45%,填空题占15%,解答题占40%。
试题按其难度分为容易题,中档题和稍难题。其中难度值为0.8以上的试题为容易题,约占80%;难度值为0.6-0.8之间的试题为中档题,约占10%;难度值为0.4-0.6之间的试题为较难题,约占10%;不出现难度值为0.3以下的试题。试卷的总体难度控制在0.8左右。
考试采用闭卷笔试的形式,全卷100分,考试时间90分钟。
(三)不等式
1.不等关系与一元二次不等式
了解不等式(组)的实际背景,会从实际问题的情境中抽象出不等式模型;了解一元二次不等式与相应的二次函数、一元二次方程的联系;会解一元二次不等式。
2.二元一次不等式组与简单线性规划问题
会从实际情境中抽象出二元一次不等式组;了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组;会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决。
3.基本不等式: 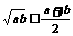 (a,b≥0)
(a,b≥0)
了解基本不等式的证明过程;会用基本不等式解决简单的最大(小)值问题。
(二)数列
1.数列的概念和简单表示法
了解数列的概念和几种简单的表示方法(列表、图象、通项公式);知道数列是自变量为正整数的特殊函数。
2.等差数列、等比数列
理解等差数列、等比数列的概念;掌握等差数列、等比数列的通项公式与前n项和公式;能判断数列的等差或等比关系,并用等差数列、等比数列的有关知识解决相应的问题;了解等差数列与一次函数的关系,等比数列与指数函数的关系。
(一)解三角形
1.正弦定理和余弦定理
掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题。
2.正弦定理和余弦定理的应用
能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
(十)三角恒等变换
1.两角和与差的三角函数公式
会用向量的数量积推导出两角差的余弦公式;会用两角差的余弦公式推导出两角和的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式,了解它们的内在联系。
2.简单的三角恒等变换
能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但不要求记忆)。
(九)平面向量
1.平面向量的实际背景及基本概念
了解向量的实际背景;理解平面向量概念和两个向量相等的含义;理解向量的几何表示。
2.向量的线性运算
掌握向量加、减法的运算,理解其几何意义;掌握向量数乘运算及其几何意义,理解两个向量共线的含义;了解向量的线性运算性质及其几何意义。
3.平面向量的基本定理及坐标表示
了解平面向量的基本定理及其意义;掌握平面向量的正交分解及其坐标表示;会用坐标表示平面向量的加法、减法与数乘运算;理解用坐标表示的平面向量共线的条件。
4.平面向量的数量积
理解平面向量数量积的含义及其物理意义;了解平面向量的数量积与向量投影的关系;掌握数量积的坐标表达式,会进行平面向量数量积的运算;会运用数量积表示两个向量的夹角,会判断两个平面向量的垂直关系。
5.向量的应用
会用向量方法解决一些简单的平面几何问题;会用向量方法解决简单的力学问题与其他一些实际问题。
(八)基本初等函数Ⅱ(三角函数)
1.任意角、弧度
了解任意角的概念和弧度制的概念;能进行弧度与角度的互化。
2.三角函数
理解任意角三角函数(正弦、余弦、正切)的定义;能用单位圆中的三角函数线推导出 的正弦、余弦、正切的诱导公式及
的正弦、余弦、正切的诱导公式及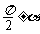 的正弦、余弦的诱导公式;能画出y=sin x, y=cos
x, y=tan x的图象,了解三角函数的周期性;理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴交点等),理解正切函数在(
的正弦、余弦的诱导公式;能画出y=sin x, y=cos
x, y=tan x的图象,了解三角函数的周期性;理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴交点等),理解正切函数在( )上的单调性;理解同角三角函数的基本关系式:sin2x+cos2x=1,
)上的单调性;理解同角三角函数的基本关系式:sin2x+cos2x=1,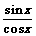 =tan x;了解函数
=tan x;了解函数
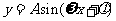 的实际意义,了解函数
的实际意义,了解函数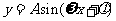 中参数A,
中参数A,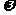 ,
,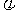 对函数图象变化的影响;会用三角函数解决一些简单实际问题。
对函数图象变化的影响;会用三角函数解决一些简单实际问题。
(七)概率
1. 事件与概率
了解随机事件发生的不确定性和频率的稳定性,了解概率的意义及频率与概率的区别;了解两个互斥事件的概率加法公式。
2.古典概型
理解古典概型及概率计算公式;会计算一些随机事件的基本事件数及其发生的概率。
3.随机数与几何概型
了解随机数的意义,了解几何概型的意义,能运用模拟方法估计概率。
(六)统计
1. 随机抽样
理解随机抽样;会用简单随机抽样方法从总体中抽取样本;了解分层抽样和系统抽样方法。
2. 用样本估计总体
了解分布的意义和作用,能根据频率分布表画频率分布直方图、频率折线图、茎叶图,了解他们各自的特点;理解样本数据标准差的意义和作用,会计算数据标准差(不要求记忆公式);能从样本数据中提取基本的数字特征(如平均数、标准差),并作出合理的解释;会用样本的频率分布估计总体分布,会用样本的基本数字特征估计总体的基本数字特征,理解样本估计总体的思想;会用随机抽样的基本方法和样本估计总体的思想,解决一些简单的实际问题。
3. 变量的相关性
会作两个有关联变量的数据的散点图,并利用散点图认识变量间的相关关系;了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程(线性回归方程系数公式不要求记忆)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com