
2、进一步熟练掌握等差数列的通项公式、性质及应用.
1、掌握"判断数列是否为等差数列"常用的方法;
Ⅰ.课题导入
[创设情境]
提问:前面我们学习了如何测量距离和高度,这些实际上都可转化已知三角形的一些边和角求其余边的问题。然而在实际的航海生活中,人们又会遇到新的问题,在浩瀚无垠的海面上如何确保轮船不迷失方向,保持一定的航速和航向呢?今天我们接着探讨这方面的测量问题。
Ⅱ.讲授新课
[范例讲解]
例1、如图,一艘海轮从A出发,沿北偏东75 的方向航行67.5 n mile后到达海岛B,然后从B出发,沿北偏东32
的方向航行67.5 n mile后到达海岛B,然后从B出发,沿北偏东32 的方向航行54.0 n mile后达到海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?(角度精确到0.1
的方向航行54.0 n mile后达到海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离?(角度精确到0.1 ,距离精确到0.01n mile)
,距离精确到0.01n mile)

学生看图思考并讲述解题思路
分析:首先根据三角形的内角和定理求出AC边所对的角 ABC,即可用余弦定理算出AC边,再根据正弦定理算出AC边和AB边的夹角
ABC,即可用余弦定理算出AC边,再根据正弦定理算出AC边和AB边的夹角 CAB。
CAB。
解:在 ABC中,
ABC中, ABC=180
ABC=180 - 75
- 75 + 32
+ 32 =137
=137 ,根据余弦定理,
,根据余弦定理,
AC= =
= ≈113.15
≈113.15
根据正弦定理, =
=  sin
sin CAB =
CAB =  =
=  ≈0.3255,
≈0.3255,
所以  CAB =19.0
CAB =19.0 ,
75
,
75 -
-  CAB =56.0
CAB =56.0
答:此船应该沿北偏东56.1 的方向航行,需要航行113.15n
mile
的方向航行,需要航行113.15n
mile
例2、在某点B处测得建筑物AE的顶端A的仰角为 ,沿BE方向前进30m,至点C处测得顶端A的仰角为2
,沿BE方向前进30m,至点C处测得顶端A的仰角为2 ,再继续前进10
,再继续前进10 m至D点,测得顶端A的仰角为4
m至D点,测得顶端A的仰角为4 ,求
,求 的大小和建筑物AE的高。
的大小和建筑物AE的高。

解法一:(用正弦定理求解)由已知可得在 ACD中,
ACD中,
AC=BC=30,
AD=DC=10 ,
,  ADC =180
ADC =180 -4
-4 ,
,

 =
= 。 因为 sin4
。 因为 sin4 =2sin2
=2sin2 cos2
cos2
 cos2
cos2 =
= ,得 2
,得 2 =30
=30

 =15
=15 ,
,  在Rt
在Rt ADE中,AE=ADsin60
ADE中,AE=ADsin60 =15
=15
答:所求角 为15
为15 ,建筑物高度为15m
,建筑物高度为15m
解法二:(设方程来求解)设DE= x,AE=h
在 Rt ACE中,(10
ACE中,(10 + x)
+ x) + h
+ h =30
=30 在 Rt
在 Rt ADE中,x
ADE中,x +h
+h =(10
=(10 )
)
两式相减,得x=5 ,h=15
,h=15  在 Rt
在 Rt ACE中,tan2
ACE中,tan2 =
= =
=
 2
2 =30
=30 ,
, =15
=15
答:所求角 为15
为15 ,建筑物高度为15m
,建筑物高度为15m
解法三:(用倍角公式求解)设建筑物高为AE=8,由题意,得
 BAC=
BAC= ,
,  CAD=2
CAD=2 , AC = BC =30m , AD = CD =10
, AC = BC =30m , AD = CD =10 m
m
在Rt ACE中,sin2
ACE中,sin2 =
= ------ ① 在Rt
------ ① 在Rt ADE中,sin4
ADE中,sin4 =
= , ---- ②
, ---- ②
② ① 得 cos2
① 得 cos2 =
= ,2
,2 =30
=30 ,
, =15
=15 ,AE=ADsin60
,AE=ADsin60 =15
=15
答:所求角 为15
为15 ,建筑物高度为15m
,建筑物高度为15m
例3、某巡逻艇在A处发现北偏东45 相距9海里的C处有一艘走私船,正沿南偏东75
相距9海里的C处有一艘走私船,正沿南偏东75 的方向以10海里/小时的速度向我海岸行驶,巡逻艇立即以14海里/小时的速度沿着直线方向追去,问巡逻艇应该沿什么方向去追?需要多少时间才追赶上该走私船?
的方向以10海里/小时的速度向我海岸行驶,巡逻艇立即以14海里/小时的速度沿着直线方向追去,问巡逻艇应该沿什么方向去追?需要多少时间才追赶上该走私船?

师:你能根据题意画出方位图?教师启发学生做图建立数学模型
分析:这道题的关键是计算出三角形的各边,即需要引入时间这个参变量。
解:如图,设该巡逻艇沿AB方向经过x小时后在B处追上走私船,则CB=10x, AB=14x,AC=9,
 ACB=
ACB= +
+ =
=
 (14x)
(14x)  = 9
= 9 + (10x)
+ (10x)  -2
-2 9
9 10xcos
10xcos
 化简得32x
化简得32x -30x-27=0,即x=
-30x-27=0,即x= ,或x=-
,或x=- (舍去)
(舍去)
所以BC = 10x =15,AB =14x =21,
又因为sin BAC =
BAC = =
=

 =
=

 BAC =38
BAC =38 ,或
,或 BAC =141
BAC =141 (钝角不合题意,舍去),
(钝角不合题意,舍去),
 38
38 +
+ =83
=83
答:巡逻艇应该沿北偏东83 方向去追,经过1.4小时才追赶上该走私船.
方向去追,经过1.4小时才追赶上该走私船.
评注:在求解三角形中,我们可以根据正弦函数的定义得到两个解,但作为有关现实生活的应用题,必须检验上述所求的解是否符合实际意义,从而得出实际问题的解
Ⅲ.课堂练习
课本第16页练习
Ⅳ.课时小结
解三角形的应用题时,通常会遇到两种情况:
(1)已知量与未知量全部集中在一个三角形中,依次利用正弦定理或余弦定理解之。
(2)已知量与未知量涉及两个或几个三角形,这时需要选择条件足够的三角形优先研究,再逐步在其余的三角形中求出问题的解。
Ⅴ.课后作业
《习案》作业六
重点:能根据正弦定理、余弦定理的特点找到已知条件和所求角的关系
难点:灵活运用正弦定理和余弦定理解关于角度的问题
3、培养学生提出问题、正确分析问题、独立解决问题的能力,并激发学生的探索精神。
2、通过综合训练强化学生的相应能力,让学生有效、积极、主动地参与到探究问题的过程中来,逐步让学生自主发现规律,举一反三。
1、能够运用正弦定理、余弦定理等知识和方法解决一些有关计算角度的实际问题
(1)定理的表示形式: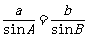

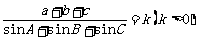 ;
;
或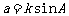 ,
,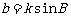 ,
,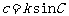

(2)正弦定理的应用范围:
①已知两角和任一边,求其它两边及一角;
②已知两边和其中一边对角,求另一边的对角。
[探索研究]
在初中,我们已学过如何解直角三角形,下面就首先来探讨直角三角形中,角与边的等式关系。如图,在Rt ABC中,设BC=a,AC=b,AB=c, 根据锐角三角函数中正弦函数的定义,
ABC中,设BC=a,AC=b,AB=c, 根据锐角三角函数中正弦函数的定义,
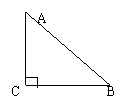 有
有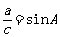 ,
,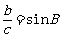 ,又
,又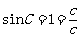 ,
,
则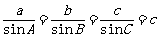
从而在直角三角形ABC中,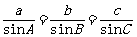
思考1:那么对于任意的三角形,以上关系式是否仍然成立?(由学生讨论、分析)
可分为锐角三角形和钝角三角形两种情况:
 如图1.1-3,(1)当
如图1.1-3,(1)当 ABC是锐角三角形时,设边AB上的高是CD,根据任意角三角函数的定义,
ABC是锐角三角形时,设边AB上的高是CD,根据任意角三角函数的定义,
有CD=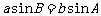 ,则
,则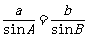 ,
C
,
C
同理可得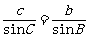 ,
b
a
,
b
a
 从而
从而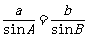
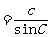 A
c B
A
c B
(2)当 ABC是钝角三角形时,以上关系式仍然成立。(由学生课后自己推导)
ABC是钝角三角形时,以上关系式仍然成立。(由学生课后自己推导)
思考2:还有其方法吗?
由于涉及边长问题,从而可以考虑用向量来研究这问题。
(证法二):过点A作单位向量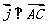 , 由向量的加法可得
, 由向量的加法可得 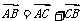
则 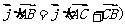
 ∴
∴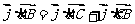
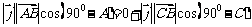
∴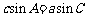 ,即
,即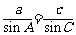
同理,过点C作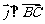 ,可得
,可得 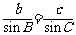 从而
从而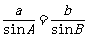
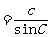
从上面的研探过程,可得以下定理
正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即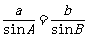
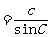
[理解定理]
(1)正弦定理说明同一三角形中,边与其对角的正弦成正比,且比例系数为同一正数,
即存在正数k使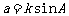 ,
,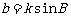 ,
,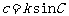 ;
;
(2)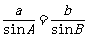
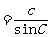 等价于
等价于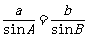 ,
,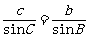 ,
,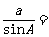
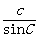
思考:正弦定理的基本作用是什么?
①已知三角形的任意两角及其一边可以求其他边,如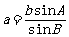 ;
;
②已知三角形的任意两边与其中一边的对角可以求其他角的正弦值,如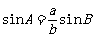 。
。
一般地,已知三角形的某些边和角,求其他的边和角的过程叫作解三角形。
[例题分析]
例1.在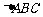 中,已知
中,已知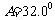 ,
,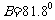 ,
,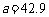 cm,解三角形。
cm,解三角形。
解:根据三角形内角和定理,
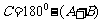
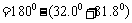
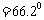 ;
;
根据正弦定理,
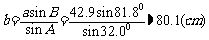 ;
;
根据正弦定理, 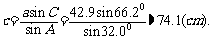
评述:对于解三角形中的复杂运算可使用计算器。
练习:在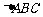 中,已知下列条件解三角形。
中,已知下列条件解三角形。
(1)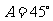 ,
,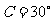 ,
,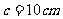 , (2)
, (2)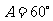 ,
,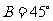 ,
,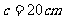
例2. 在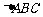 中,已知
中,已知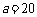 cm,
cm,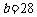 cm,
cm,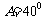 ,解三角形(角度精确到
,解三角形(角度精确到 ,边长精确到1cm)。
,边长精确到1cm)。
解:根据正弦定理,
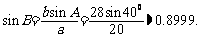 因为
因为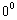 <
<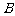 <
<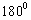 ,所以
,所以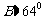 ,或
,或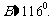
⑴ 当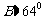 时,
时, 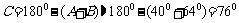 ,
,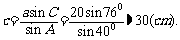
⑵ 当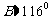 时,
时,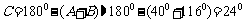 ,
,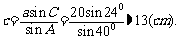
应注意已知两边和其中一边的对角解三角形时,可能有两解的情形。
课堂练习
第4页练习第2题。
思考题:在 ABC中,
ABC中,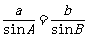
 ,这个k与
,这个k与 ABC有什么关系?
ABC有什么关系?
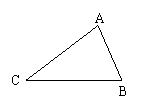 如图1.1-1,固定
如图1.1-1,固定 ABC的边CB及
ABC的边CB及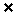 B,使边AC绕着顶点C转动。
B,使边AC绕着顶点C转动。
思考: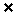 C的大小与它的对边AB的长度之间有怎样的数量关系?
C的大小与它的对边AB的长度之间有怎样的数量关系?
显然,边AB的长度随着其对角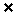 C的大小的增大而增大。
C的大小的增大而增大。
能否用一个等式把这种关系精确地表示出来?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com