3、会用等差数列的前n项和公式解决一些简单的与前n项和有关的问题．

2、等差数列前n项和公式及其获取思路；

1、等差数列前n项和公式．

1. 等差数列的性质；　 2. 判断数列是否为等差数列常用的方法．

2．判断数列是否为等差数列的常用方法：

(1) 定义法: 证明a_n-a_n-1=d (常数)

例2. 已知数列{a_n}的前n项和为S_n=3n²-2n, 求证数列{a_n}成等差数列,并求其首项、公差、通项公式.

解: 当n=1时,a₁=S₁=3﹣2=1; 　 当n≥2时,a_n=Sn﹣S_n﹣1=3n²﹣2n﹣ [3(n﹣1)²﹣2(n﹣1)]=6n﹣5;

　 ∵n=1时a₁满足a_n=6n﹣5,∴a_n=6n﹣5

　 首项a₁=1,a_n﹣a_n﹣1=6(常数)

　 ∴数列{a_n}成等差数列且公差为6.

(2)中项法: 利用中项公式, 若2b=a+c,则a, b, c成等差数列.

(3)通项公式法: 等差数列的通项公式是关于n的一次函数.

例3. 已知数列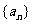的通项公式为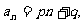其中p、q为常数，且p≠0，那么这个数列一定是等差数列吗？

分析：判定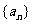是不是等差数列，可以利用等差数列的定义，也就是看(n＞1)是不是一个与n无关的常数。

解：取数列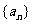中的任意相邻两项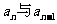(n＞1)，

求差得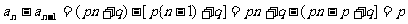

　　 它是一个与n无关的数.

所以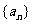是等差数列。

课本左边“旁注”：这个等差数列的首项与公差分别是多少？

这个数列的首项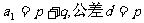。由此我们可以知道对于通项公式是形如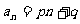的数列，一定是等差数列，一次项系数p就是这个等差数列的公差，首项是p+q.

如果一个数列的通项公式是关于正整数n的一次型函数，那么这个数列必定是等差数列。

[探究]

引导学生动手画图研究完成以下探究：

⑴在直角坐标系中，画出通项公式为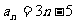的数列的图象。这个图象有什么特点？

⑵在同一个直角坐标系中，画出函数y=3x-5的图象，你发现了什么？据此说一说等差数列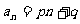与一次函数y=px+q的图象之间有什么关系。

分析：⑴n为正整数，当n取1，2，3，……时，对应的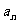可以利用通项公式求出。经过描点知道该图象是均匀分布的一群孤立点；

⑵画出函数y=3x-5的图象一条直线后发现数列的图象(点)在直线上，数列的图象是改一次函数当x在正整数范围内取值时相应的点的集合。于是可以得出结论：等差数列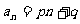的图象是一次函数y=px+q的图象的一个子集，是y=px+q定义在正整数集上对应的点的集合。

该处还可以引导学生从等差数列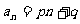中的p的几何意义去探究。

1．性质：在等差数列{a_n}中,若m + n=p + q, 则a_m + a_n = a_p + a_q

特别地,若m+n=2p, 则a_m+a_n=2a_p

例1. 在等差数列{a_n}中

　　　 (1) 若a₅=a, a₁₀=b, 求a₁₅;

　　　 (2) 若a₃+a₈=m, 求a₅+a₆;

　　　 (3) 若a₅=6, a₈=15, 求a₁₄;

　　　 (4) 若a₁+a₂+…+a₅=30, a₆+a₇+…+a₁₀=80,求a₁₁+a₁₂+…+a₁₅.

解: (1) 2a₁₀=a₅+a₁₅,即2b=a+a₁₅ ,　 ∴a₁₅=2b﹣a;

(2) ∵5+6=3+8=11,∴a₅+a₆=a₃+a=m

(3) a8=a₅+(8﹣3)d, 即15=6+3d, ∴d=3，从而a₁₄=a₅+(14-5)d=6+9×3=33

(一)、复习

1．等差数列的定义．

2．等差数列的通项公式：

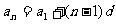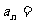
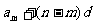　 (或 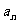=pn+q (p、q是常数))

3．有几种方法可以计算公差d:

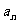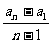① d=－　　 ② d=　　 ③ d=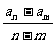　　

4.　 {a_n}是首项a1=1, 公差d=3的等差数列, 若a_n =2005,则n =(　　 )　　　　　　 　 A. 667　　　 　B. 668　　 　C. 669　　　　 D. 670

5. 在3与27之间插入7个数,　 使它们成为等差数列,则插入的7个数的第四个数是(　　 )

　 A. 18　　　 　B. 9　　　　 C. 12　　　　 　D. 15　　　　　　　　

重点：等差数列的通项公式、性质及应用．

难点：灵活应用等差数列的定义及性质解决一些相关问题．

3、进一步熟练掌握等差数列的通项公式、性质及应用．