
1、等差数列求和公式: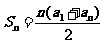 ,
,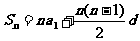
2.《习案》作业十三.
2.等差数列的前n项和公式2: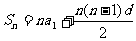 .
.
1.等差数列的前n项和公式1: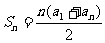 ;
;
例1、(1)已知等差数列{an}中, a1 =4, S8 =172,求a8和d ;
(2)等差数列-10,-6,-2,2,…前多少项的和是54?
解:(1) 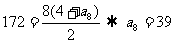
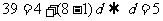
(2)设题中的等差数列为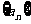 ,前n项为
,前n项为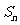 则
则 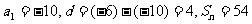
由公式可得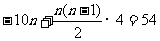 . 解之得:
. 解之得: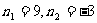 (舍去)
(舍去)
∴等差数列-10,-6,-2,2…前9项的和是54.
例2、教材P43面的例1
解:
例3.求集合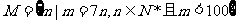 的元素个数,并求这些元素的和.
的元素个数,并求这些元素的和.
解:由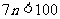 得
得 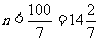
∴正整数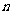 共有14个即
共有14个即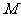 中共有14个元素
中共有14个元素
即:7,14,21,…,98 是
 等差数列.
等差数列.
∴  答:略.
答:略.
例4、等差数列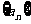 的前
的前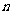 项和为
项和为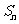 ,若
,若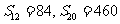 ,求
,求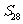 .
.
(学生练 学生板书
学生板书 教师点评及规范)
教师点评及规范)
练习:⑴在等差数列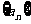 中,已知
中,已知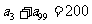 ,求
,求 .
.
⑵在等差数列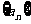 中,已知
中,已知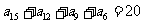 ,求
,求 .
.
例4.已知等差数列{an}前四项和为21,最后四项的和为67,所有项的和为286,求项数n.
解:依题意,得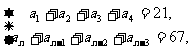
两式相加得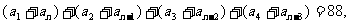
又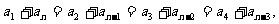 所以
所以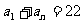
又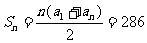 ,所以n=26.
,所以n=26.
例5.已知一个等差数列{an}前10项和为310,前20项的和为1220,由这些条件能确定这个等差数
列的前n项的和吗?.
思考:(1)等差数列中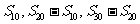 ,成等差数列吗?
,成等差数列吗?
(2)等差数列前m项和为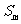 ,则
,则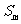 、
、 .、
.、 是等差数列吗?
是等差数列吗?
练习:教材第118页练习第1、3题.
2. 等差数列的前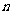 项和公式2:
项和公式2: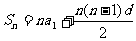 .
.
用上述公式要求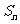 必须具备三个条件:
必须具备三个条件: .
.
但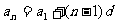 代入公式1即得:
代入公式1即得:
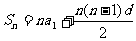
此公式要求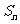 必须已知三个条件:
必须已知三个条件: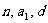
总之:两个公式都表明要求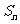 必须已知
必须已知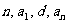 中三个.
中三个.
公式二又可化成式子: 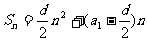 ,当d≠0,是一个常数项为零的二次式.
,当d≠0,是一个常数项为零的二次式.
1.等差数列的前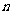 项和公式1:
项和公式1: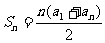
证明: 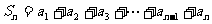 ①
①
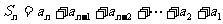 ②
②
①+②: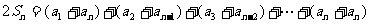
∵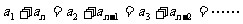
∴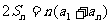 由此得:
由此得: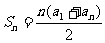 .
.
(一)、复习引入:
1.等差数列的定义:
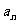 -
- =d ,(n≥2,n∈N
=d ,(n≥2,n∈N )
)
2.等差数列的通项公式:
(1)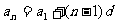 (2)
(2)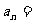
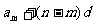 (3)
(3)
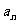 =pn+q (p、q是常数)
=pn+q (p、q是常数)
3.几种计算公差d的方法:① 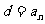 -
- ②
② 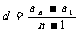 ③
③ 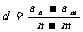
4.等差中项: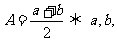 成等差数列
成等差数列
5.等差数列的性质: m+n=p+q 
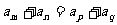 (m, n, p, q ∈N )
(m, n, p, q ∈N )
6.数列的前n项和:数列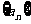 中,
中,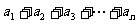 称为数列
称为数列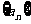 的前n项和,记为
的前n项和,记为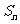 .
.
“小故事”1、2、3
高斯是伟大的数学家,天文学家,高斯十岁时,有一次老师出了一道题目,老师说: “现在给大家出道题目: 1+2+…100=?”
过了两分钟,正当大家在:1+2=3;3+3=6;4+6=10…算得不亦乐乎时,高斯站起来回答说:
 “1+2+3+…+100=5050.”
“1+2+3+…+100=5050.”
教师问:“你是如何算出答案的?”
高斯回答说:“因为1+100=101;
2+99=101;…50+51=101,所以 101×50=5050”
这个故事告诉我们:
(1)作为数学王子的高斯从小就善于观察,敢于思考,所以他能从一些简单的事物中发现和寻找出某些规律性的东西.
(2)该故事还告诉我们求等差数列前n项和的一种很重要的思想方法,这就是下面我们要介绍的“倒序相加”法.
教学难点:灵活应用等差数列前n项公式解决一些简单的有关问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com