
下面我们来看这样几个数列,看其又有何共同特点?(教材上的P48面)
1,2,4,8,16,…,263; ① 1,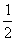 ,
,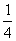 ,
,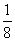 ,…;
②
,…;
②
1,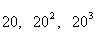 ,…; ③
,…; ③ 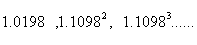 ④
④
对于数列①,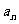 =
=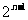 ;
; 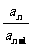 =2(n≥2).对于数列②,
=2(n≥2).对于数列②,
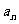 =
=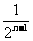 ;
; (n≥2).
(n≥2).
对于数列③,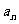 =
=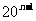 ;
; 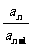 =20(n≥2).
=20(n≥2).
共同特点:从第二项起,第一项与前一项的比都等于同一个常数.
5.已知等差数列{an},3 a5 =8 a12, a1<0,设前n项和为Sn,求Sn取最小值时n的值.
[分析]求等差数列前n项的和最小,可以用函数的方式去求,亦可以用数列单调性,也可以由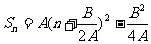 完成.
完成.
解法一:
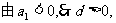
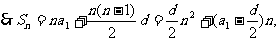
点(n,Sn)是开口向上抛物线上一些孤立的点,即在函数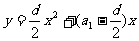 的图象上,其对称轴
的图象上,其对称轴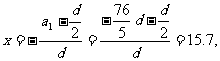 距离x=15.7最近的整数点(16,S16),
距离x=15.7最近的整数点(16,S16), 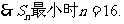
解法二: 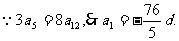
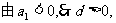
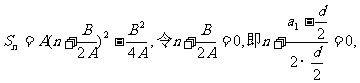
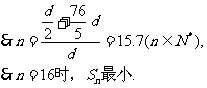
4.已知等差数列{an},满足an =40-4n ,求前多少项的和最大?最大值是多少?
解法一:由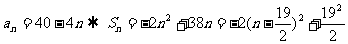

解法二: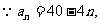
令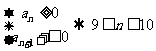
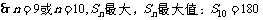 .
.
3.首项为正数的等差数列{an},它的前3项之和与前11项之和相等,问此数列前多少项之和最大?
解法一:由S3=S11
得: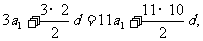 解之得
解之得
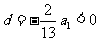
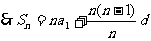
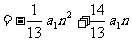
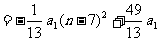
故当n=7时, Sn 最大,即前7项之和最大.
解法二:由 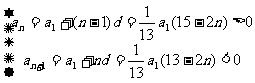
解得: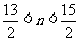 ,所以n=7,即前7项之和最大.
,所以n=7,即前7项之和最大.
解法三:由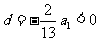 知: {an}是递减的等差数列.
知: {an}是递减的等差数列.
又S3=S11,
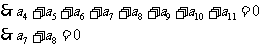
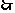 必有
必有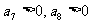 ,
,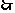 前7项之和最大.
前7项之和最大.
2. 数列{an}是首项为正数a1的等差数列,又S9= S17.问数列的前几项和最大?
解:由S9= S17得9a5=17 a9,

说明: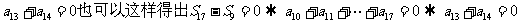 .
.
作业:《习案》作业十四。
补充题:(依情况而定)
1.(1)已知等差数列{an}的an=24-3n,则前多少项和最大?
(2)已知等差数列{bn}的通项bn=2n-17,则前多少项和最小?
解:(1)由an=24-3n知当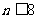 时,
时,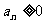 ,当
,当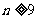 时,
时,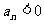 ,
,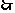 前8项或前7项的和取最大值.
前8项或前7项的和取最大值.
(2)由bn=2n-17n知当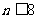 时,
时,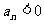 ,当
,当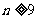 时,
时,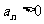 ,
, 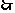 前8项的和取最小值.
前8项的和取最小值.
求"等差数列前n项和的最值问题"常用的方法有:
(1)满足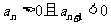 的n值;
的n值;
(2)由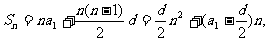 利用二次函数的性质求n的值;
利用二次函数的性质求n的值;
(3)利用等差数列的性质求.
2. 教学等差数列前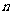 项和的最值问题:
项和的最值问题:
① 例题讲解:
例2、数列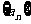 是等差数列,
是等差数列,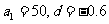 . (1)从第几项开始有
. (1)从第几项开始有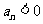 ;(2)求此数列的前
;(2)求此数列的前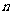 项和的最大值.
项和的最大值.
结论:等差数列前项和的最值问题有两种方法:
(1)
当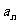 >0,d<0,前n项和有最大值
>0,d<0,前n项和有最大值 可由
可由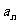 ≥0,且
≥0,且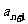 ≤0,求得n的值;
≤0,求得n的值;
当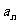 <0,d>0,前n项和有最小值
<0,d>0,前n项和有最小值 可由
可由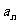 ≤0,且
≤0,且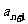 ≥0,求得n的值.
≥0,求得n的值.
(2)由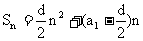 利用二次函数配方法求得最值时n的值.
利用二次函数配方法求得最值时n的值.
练习:在等差数列{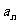 }中,
}中, 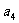 =-15, 公差d=3, 求数列{
=-15, 公差d=3, 求数列{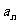 }的前n项和
}的前n项和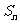 的最小值.
的最小值.
例3、已知等差数列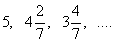 的前n项的和为
的前n项的和为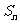 ,求使得
,求使得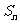 最大的序号n的值。
最大的序号n的值。
归纳:(1)当等差数列{an}首项为正数,公差小于零时,它的前n项的和为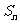 有最大值,可以通过
有最大值,可以通过
 求得n
求得n
(2)当等差数列{an}首项不大于零,公差大于零时,它的前n项的和为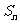 有最小值,可以通过
有最小值,可以通过
 求得n
求得n
1、探究:等差数列的前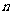 项和公式是一个常数项为零的二次式.
项和公式是一个常数项为零的二次式.
例1、已知数列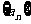 的前
的前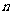 项和为
项和为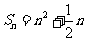 ,求这个数列的通项公式. 这个数列是等差数列吗?如果是,它的首项与公差分别是什么?
,求这个数列的通项公式. 这个数列是等差数列吗?如果是,它的首项与公差分别是什么?
[结论]数列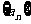 的前
的前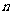 项和
项和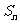 与
与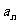 的关系:
的关系:
由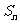 的定义可知,当n=1时,
的定义可知,当n=1时,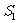 =
=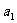 ;当n≥2时,
;当n≥2时,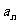 =
=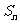 -
-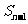 ,即
,即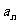 =
=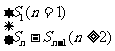 .
.
练习:已知数列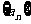 的前
的前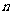 项和
项和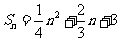 ,求该数列的通项公式. 这个数列是等差数列吗?
,求该数列的通项公式. 这个数列是等差数列吗?
探究:一般地,如果一个数列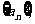 的前n项和为
的前n项和为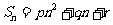 ,其中p、q、r为常数,且
,其中p、q、r为常数,且 ,那么这个数列一定是等差数列吗?如果是,它的首项与公差分别是多少?
,那么这个数列一定是等差数列吗?如果是,它的首项与公差分别是多少?
(是,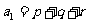 ,
,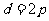 ).
).
由此,等差数列的前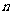 项和公式
项和公式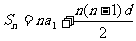 可化成式子:
可化成式子: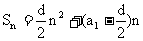 ,当d≠0,是一个常数项为零的二次式.
,当d≠0,是一个常数项为零的二次式.
2、在等差数列{an}中 (1) 若a5=a, a10=b, 求a15; (2) 若a3+a8=m, 求a5+a6; (3) 若a5=6, a8=15, 求a14; (4) 若a1+a2+…+a5=30, a6+a7+…+a10=80,求a11+a12+…+a15.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com