2.　等比数列的通项公式:　

， 　　，　

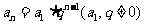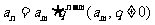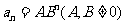
1．等比数列的定义．

2.《习案》作业十五．

2.等比数列的通项公式及变形式．

1.等比数列的定义；

例1．一个等比数列的第3项与第4项分别是12与18，求它的第1项与第2项.

解：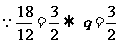　　　　　

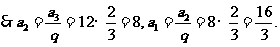
例2．求下列各等比数列的通项公式：

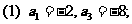
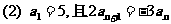
解：(1)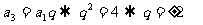

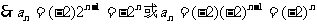
　　 (2)

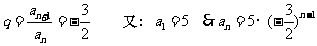
例3．教材P50面的例1。

例4．已知数列{a_n}满足，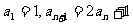

(1)求证数列{a_n+1}是等比数列；(2)求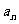的表达式。

练习：教材第52页第1、2题．

3.等比数列的通项公式2: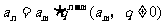

2.等比数列的通项公式1:

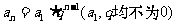
观察法：由等比数列的定义，有：；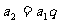

；　 ；… … … … … … …

．

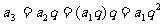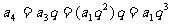　迭乘法：由等比数列的定义，有：；；；…；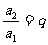

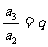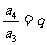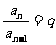
　　　所以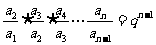，即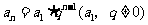

1．等比数列的定义：一般地，若一个数列从第二项起，每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列.这个常数叫等比数列的公比，用字母q表示(q≠0)，即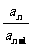：=q(q≠0).

思考：(1)等比数列中有为0的项吗？　 (2)公比为1的数列是什么数列？

　　 (3)既是等差数列又是等比数列的数列存在吗？(4)常数列都是等比数列吗？

(1)“从第二项起”与“前一项”之比为常数q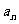； {}成等比数列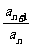=q(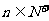，q≠0．)

(2) 隐含：任一项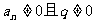

(3) q= 1时，{a_n}为常数数列．　　　 (4)．既是等差又是等比数列的数列：非零常数列．