
例1:求下列等比数列前8项的和.
(1)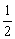 ,
,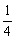 ,
,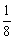 ,…
(2)
,…
(2)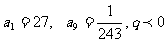
解:由a1=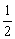 ,
,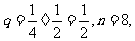 得
得 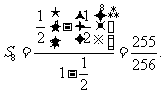
例2:某商场第一年销售计算机5000台,如果平均每年的售价比上一年增加10%,那么从第一年起,约几年内可使总销售量达到30000台(保留到个位)?
解:根据题意,每年销售量比上一年增加的百分率相同,所以从第一年起,每年的销售量组成一个等比数列{an},其中
a1=5000, 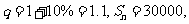 于是得到
于是得到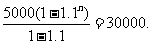
整理得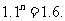 两边取对数,得
两边取对数,得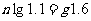 用计算器算得
用计算器算得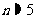 (年).
(年).
答:约5年内可以使总销售量达到30000台.
例3.求数列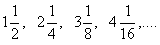 前n项的和。
前n项的和。
例4:求求数列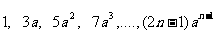 的前n项的和。
的前n项的和。
练习:教材第58面练习第1题.
(三)等比数列的前n项和公式:
当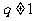 时,
时,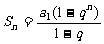 ① 或
① 或 ② 当q=1时,
② 当q=1时,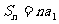
思考:什么时候用公式(1)、什么时候用公式(2)?
(当已知a1, q, n 时用公式①;当已知a1, q, an时,用公式②.)
(二)怎样求等比数列前n项的和?
公式的推导方法一:
一般地,设等比数列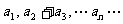 它的前n项和是
它的前n项和是 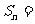
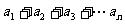
由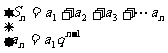 得
得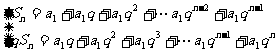
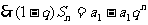 ∴当
∴当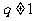 时,
时,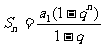 ① 或
① 或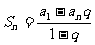 ②
②
当q=1时,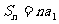
公式的推导方法二:
由定义, 由等比的性质,
由等比的性质,
即 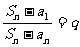

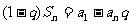 (结论同上)
(结论同上)
围绕基本概念,从等比数列的定义出发,运用等比定理,导出了公式.
公式的推导方法三:
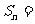
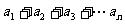 =
=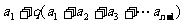 =
=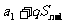 =
=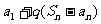

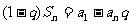 (结论同上)
(结论同上)
“方程”在代数课程里占有重要的地位,方程思想是应用十分广泛的一种数学思想,利用方程思想,在已知量和未知量之间搭起桥梁,使问题得到解决.
(一)提出问题 :关于国际相棋起源问题
例如:怎样求数列1,2,4,…262,263的各项和?
即求以1为首项,2为公比的等比数列的前64项的和,可表示为:
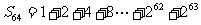 ① 2
① 2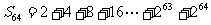 ②
②
由②-①可得: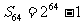
这种求和方法称为“错位相减法”, “错位相减法”是研究数列求和的一个重要方法.
4.性质:若m+n=p+q,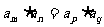
3.{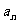 }成等比数列
}成等比数列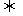
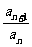 =q(
=q(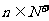 ,q≠0)
,q≠0) 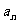 ≠0
≠0
2. 等比数列的通项公式: 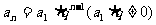 ,
, 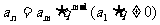
1.等比数列的定义.
2.《习案》作业十六.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com