
数列的通项公式:如果数列{an}的第n项an与n之间的关系可以用一个公式来表示,这个
公式就叫做这个数列的通项公式.
2. 作业:《学案》P41---P42面的双基训练。
思考题.设函数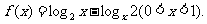 数列{an}满足
数列{an}满足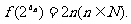
(1)求数列{an}的通项公式; (2)证明数列{an}为n的单调函数.
解:(1) 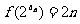 得
得
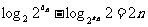 ,
即
,
即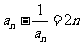
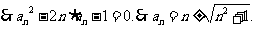
又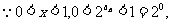
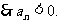 故{an}的通项公式
故{an}的通项公式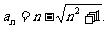
(2)证明: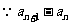
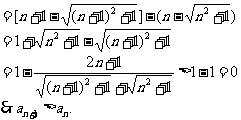
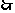 数列{an}为n的单调递增数列.
数列{an}为n的单调递增数列.
从知识结构、数学思想、数学方法和题型变化等四个方面进行复习总结.
2.题型二:等差数列的证明与计算.
例4.设Sn 为数列{an}的前n项和,已知S1 =1,且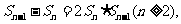
(1)求证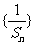 是等差数列; (2)求数列{an}的通项公式.
是等差数列; (2)求数列{an}的通项公式.
(1)证明: 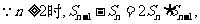
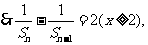
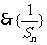 是以
是以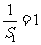 为首项,以2为公差的等差数列.
为首项,以2为公差的等差数列.
(2)解: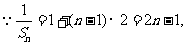
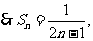
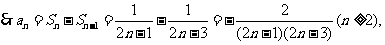
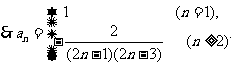
1.题型一:求数列通项公式的问题.
例1.已知数列{an}的首项a1=1,其递推公式为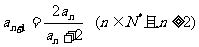 .求其前五项,并归纳出通项公式.
.求其前五项,并归纳出通项公式.
解法一: a1=1,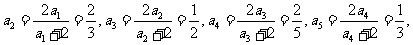 归纳得
归纳得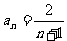
解法二: 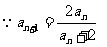 又
又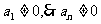
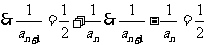
故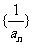 是以1为首项,
是以1为首项,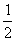 为等差的等差数列
为等差的等差数列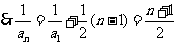
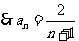 .令n=1,2,3,4,5得a1=1,
.令n=1,2,3,4,5得a1=1,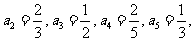
例2.数列{an}中,已知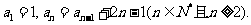 求此数列的通项公式.
求此数列的通项公式.
解: 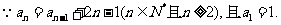

把这n-1个式子两边分别相加可得 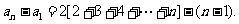
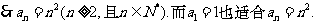 故数列{an}的通项公式为
故数列{an}的通项公式为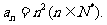
例3.数列{an}中, 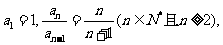 求此数列的通项公式.
求此数列的通项公式.
解: 
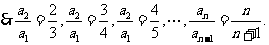
把这n-1个式子两边分别相乘可得
 即
即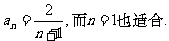
故{an}的通项公式为
(五)作业:《 习案》作业
比较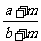 与
与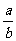 (其中
(其中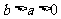 ,
,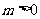 )的大小
)的大小
解: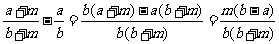 ,
,
∵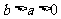 ,
,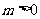 ,∴
,∴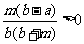 ,所以
,所以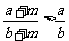 .
.
说明:不等式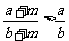 (
(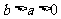 ,
,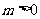 )在生活中可以找到原型:
)在生活中可以找到原型: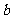 克糖水中有
克糖水中有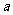 克糖(
克糖(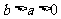 ),若再添加
),若再添加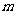 克糖(
克糖(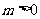 ),则糖水便甜了.
),则糖水便甜了.
(四)课堂小结
1.通过具体情景,建立不等式模型;
2.比较两实数大小的方法--求差比较法.
(三)知识拓展
1.设问:等式性质中:等式两边加(减)同一个数(或式子),结果仍相等。不等式是否也有类似的性质呢?
从实数的基本性质出发,实数的运算性质与大小顺序之间的关系:对于任意两个实数a,b,
如果a>b,那么a-b是正数; 如果a<b,那么a-b是负数; 如果a-b等于0.
它们的逆命题也是否正确?
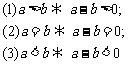
2.例3、比较(a+3)(a-5)与(a+2)(a-4)的大小.
例4、已知x≠0,比较(x2+1)2与x4+x2+1的大小.
归纳:作差比较法的步骤是:
1、作差;
2、变形:配方、因式分解、通分、分母(分子)有理化等;
3、判断符号;
4、作出结论.
(二)典例分析
例1:某校学生以面粉和大米为主食.已知面食每100克含蛋白质6个单位,含淀粉4个单位;米饭每100克含蛋白质3个单位,含淀粉7个单位.某快餐公司给学生配餐,现要求每盒至少含8个单位的蛋白质和10个单位的淀粉.设每盒快餐需面食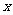 百克、米饭
百克、米饭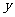 百克,试写出
百克,试写出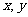 满足的条件.
满足的条件.
例2:配制 两种药剂需要甲、乙两种原料,已知配一剂
两种药剂需要甲、乙两种原料,已知配一剂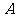 种药需甲料3毫克,乙料5毫克,配一剂
种药需甲料3毫克,乙料5毫克,配一剂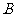 药需甲料5毫克,乙料4毫克。今有甲料20毫克,乙料25毫克,若
药需甲料5毫克,乙料4毫克。今有甲料20毫克,乙料25毫克,若 两种药至少各配一剂,则
两种药至少各配一剂,则 两种药在配制时应满足怎样的不等关系
两种药在配制时应满足怎样的不等关系
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com