
1. 等差数列这单元学习了哪些内容?
等差数列这单元学习了哪些内容?
例1、在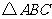 中,
中, ,
,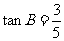 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若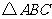 最大边的边长为
最大边的边长为 ,求最小边的边长.
,求最小边的边长.
解:(Ⅰ)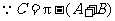 ,
, .
.
又 ,
,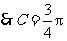 .
.
(Ⅱ) ,
,  边最大,即
边最大,即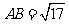 .
.
又 ,
,
 角
角 最小,
最小, 边为最小边.
边为最小边.
由 且
且 ,得
,得 .
.
由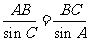 得:
得: .
所以,最小边
.
所以,最小边 .
.
例2、在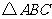 中,已知内角
中,已知内角 ,边
,边 .设内角
.设内角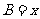 ,周长为
,周长为 .
.
(1)求函数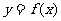 的解析式和定义域;
(2)求
的解析式和定义域;
(2)求 的最大值.
的最大值.
解:(1)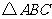 的内角和
的内角和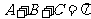 ,由
,由 得
得 .
.
应用正弦定理,知 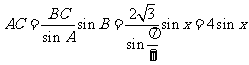 ,
,
 .
.
因为 ,所以
,所以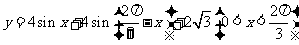 ,
,
(2)因为
 ,
,
所以,当 ,即
,即 时,
时, 取得最大值
取得最大值 .
.
例3、在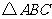 中,角
中,角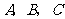 的对边分别为
的对边分别为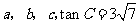 .
.
(1)求 ; (2)若
; (2)若 ,且
,且 ,求
,求 .
.
解:(1) 又
又 解得
解得 .
.
 ,
, 是锐角.
是锐角.  .
.
(2) ,
, 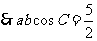 ,
,
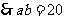 .
.
又
 .
.  .
.
 .
.
 .
.
例4、已知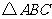 的周长为
的周长为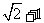 ,且
,且 .
.
(I)求边 的长;
的长;
(II)若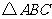 的面积为
的面积为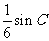 ,求角
,求角 的度数.
的度数.
解:(I)由题意及正弦定理,得 ,
,
 ,
,
两式相减,得 .
.
(II)由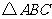 的面积
的面积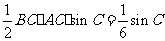 ,得
,得 ,
,
由余弦定理,得
 ,
,
所以 .
.
 知识结构:
知识结构:
2.思考题
(
(2).在数列{an}中,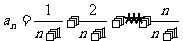 ,又
,又 ,求数列{bn}的前n项的和.
,求数列{bn}的前n项的和.
(3).在各项均为正数的等比数列中,若 的值.
的值.
解:设
由等比数列的性质  (找特殊性质项)
(找特殊性质项)
和对数的运算性质  得
得
 (合并求和)
(合并求和)
=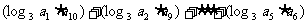
=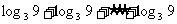
=10
1.《学案》P62面《单元检测题》
1.常用数列求和方法有:
(1) 公式法: 直接运用等差数列、等比数列求和公式;
(2) 化归法: 将已知数列的求和问题化为等差数列、等比数列求和问题;
(3) 倒序相加法: 对前后项有对称性的数列求和;
(4) 错位相减法: 对等比数列与等差数列组合数列求和;
(5) 并项求和法: 将相邻n项合并为一项求和;
(6) 分部求和法:将一个数列分成n部分求和;
(7) 裂项相消法:将数列的通项分解成两项之差,从而在求和时产生相消为零的项的求和方法.
《习案》作业二十.
2. 已知递推公式,求特殊数列的通项公式的方法:
转化为等差、等比数列求通项;累加法;迭乘法.
1. 已知数列的前几项,求数列的通项公式的方法:观察法.
题型一:已知数列的前几项,求数列的通项公式.
例1 根据数列的前几项,写出下列个数列的一个通项公式:
(1)

(2) 0.9,0.99,0.999,0.9999,…;
(3) 1,0,1,0,1,0,….
[解](1)注意到前四项中有两项分子均为4,不妨把分子都统一为4,即 ,
, ,
,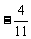 ,
,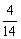 ,…观察符号是正负交替出现,因而有
,…观察符号是正负交替出现,因而有 .
.
(2) 将数列中的项和1比较,就会发现, =0.9=1-
=0.9=1-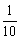
 =0.99=1-
=0.99=1- =1-
=1-
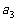 =0.999=1-
=0.999=1- =1-
=1- ,因此就有
,因此就有 .
.
(3)数列中的奇数项为1,偶数项为0,注意 的值为2和0,因此有
的值为2和0,因此有 .
.
题型二:已知递推公式,求特殊数列的通项公式.
例2 写出下面各数列一个通项公式.
(1) 练习1:
练习1: ;
;
(2)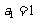 ,
, ; 练习2:
; 练习2: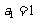 ,
, ;
;
(3)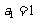 ,
, 练习3:
练习3: 
(4)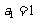 ,
, ; 练习4:
; 练习4: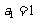 ,
,
[解](1)法一:∵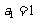 ,
, ∴
∴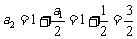 ,
,

 故
故 .
.
法二:∵ ,∴
,∴
∴{ }是一个首项为-1,公比为
}是一个首项为-1,公比为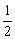 的等比数列,
的等比数列,
∴ ,即
,即 .
.
练习: ∵ ,∴
,∴  ,
,
∴{ }是以
}是以 为首项,2为公比的等比数列,
为首项,2为公比的等比数列,
∴ ,所以该数列的通项
,所以该数列的通项
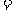
 .
.
(备用)∵ , ∴
, ∴
∴数列{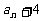 }是以2为首项,2为公比的等比数列,
}是以2为首项,2为公比的等比数列,
∴ ,即
,即 .
.
[点评]若数列{an}满足a1 =a,an+1 = pan +q (p≠1),通过变形可转化为 ,即转化为
,即转化为 是等比数列求解.
是等比数列求解.
解:(2)由 得
得 ,即
,即 ,又
,又 ,
,
∴数列{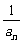 }是以1为首项,
}是以1为首项,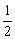 为公差的等差数列.
为公差的等差数列.
∴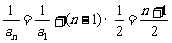 ,∴
,∴ .
.
练习2:由 得
得 , 即
, 即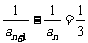 ,又
,又 ,
,
∴数列{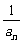 }是以1为首项,
}是以1为首项,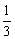 为公差的等差数列.
为公差的等差数列.
∴ ,∴
,∴ .
.
[点评]若数列{ }满足
}满足 ,
,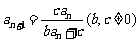 ,通过取倒可转化为
,通过取倒可转化为 ,即转化为{
,即转化为{ }是等差数列求解.
}是等差数列求解.
(3)∵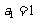 ,
, ∴
∴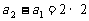
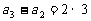
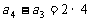 … …
… …
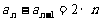
将上述(n-1)个式子相加,得
即 ,
, .
.
练习3:
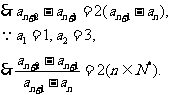
 是以
是以
 为首项,2为公比的等比数列.
为首项,2为公比的等比数列.
∴


[点评]若数列{ }满足
}满足 ,
, ,则用累加法求解,即
,则用累加法求解,即 .
.
(4)∵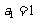 ,
, , ∴
, ∴ ,
,
∴ ,
,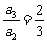 ,
, ,…,
,…,  ,
,
将上述(n-1)个式子相乘,得 ,即
,即 .
.
练习4:∵ 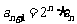 ,∴
,∴ ∴
∴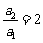 ,
, ,
, ,…,
,…, ,
,
将上述(n-1)个式子相乘,得 ,即
,即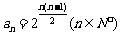 .
.
[点评]若数列{ }满足
}满足 ,
, ,则用迭乘法求解,即
,则用迭乘法求解,即 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com