
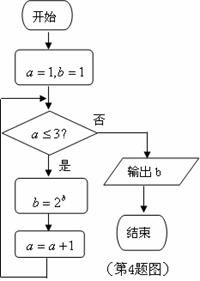
4.如右程序框图,输出的结果为( )
A.1 B.2
C.4 D.16
3.“ ”是“直线
”是“直线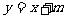 与圆
与圆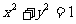 相切”的( )
相切”的( )
 A.充分而不必要条件 B.必要而不充分条件
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2.向量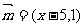 ,
,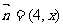 ,
,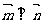 ,则
,则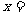 ( )
( )
A.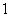 B.
B. 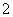 C.
C.  D.
D. 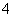
1.若集合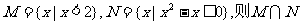 =(
)
=(
)
A.[0,1] B.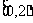 C.
C.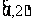 D.
D.
22.(本小题满分15分)
(Ⅰ)设M,N为短轴的两个三等分点,因为△MNF为正三角形,
所以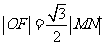 , 即1=
, 即1=
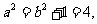 因此,椭圆方程为
因此,椭圆方程为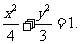 (5分)
(5分)
(Ⅱ)由题意可得抛物线方程为: (7分)
(7分)
设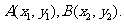 ,
, 直线
直线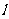 不可能为
不可能为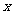 轴,故可设直线
轴,故可设直线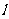 为
为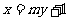
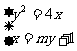 ,
,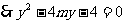
由韦达定理可得: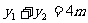 ,
,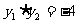 (9分)
(9分)
 的面积
的面积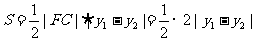 ,
,
又
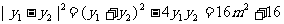 , (13分)
, (13分)
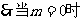 ,
, 取到最小值16,即
取到最小值16,即 的最小值为4
的最小值为4
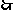
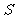 最小值为4
最小值为4
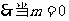 ,即直线
,即直线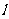 垂直
垂直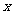 轴时,
轴时,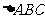 面积最小,最小值为4 (15分)
面积最小,最小值为4 (15分)
21.(本小题满分15分)
解:(1)f(x)=ax3 4ax2+4ax
4ax2+4ax
f/(x)=3ax2 8ax+4a=a(3x
8ax+4a=a(3x 2)(x
2)(x 2)=0
2)=0 x=
x=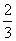 或2
或2
∵f(x)有极大值32,而f(2)=0 ∴f(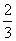 )=
)=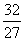 ,a =1 (7分)
,a =1 (7分)
(2)f/(x)=a(3x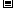 2)(x
2)(x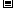 2)
2)
当a>0时,f(x)在[ 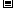 2,
2,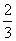 ]上递增,在[
]上递增,在[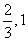 ]上递减,
]上递减,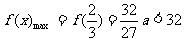 ,
,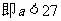
∴0<a<27 (10分)
当a<0时,f(x)在[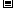 2,
2,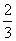 ]上递减,在[
]上递减,在[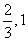 ]上递增,f(
]上递增,f( 2)=
2)=
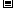 32a>f (1)=a
32a>f (1)=a
 ,即
,即 ∴
∴ 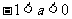 (13分)
(13分)
综上 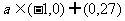 (15分)
(15分)
20.(本小题满分14分)
解:(1) (2分)
(2分)
当 时,
时,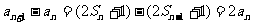 (4分)
(4分)
∴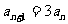 ,即
,即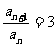
∴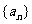 是公比为3的等比数列 (6分)
是公比为3的等比数列 (6分)
(2)由(1)得: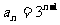 (8分)
(8分)
设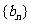 的公差为
的公差为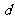 (
( ), ∵
), ∵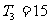 ,∴
,∴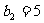 (10分)
(10分)
依题意有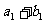 ,
,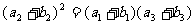 ,
,
∴
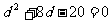 ,得
,得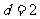 ,或
,或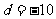 (舍去) (12分)
(舍去) (12分)
故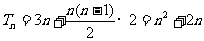 (14分)
(14分)
19. (本小题满分14分)
解:(1)由已知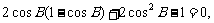
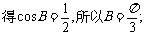 (7分)
(7分)
(2)由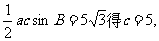 (10分)
(10分)
由余弦定理得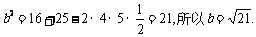 (14分)
(14分)
18.(本小题满分14分)
解:
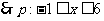 ,
,
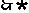
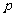 :
: (4分)
(4分)
 ,又
,又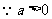 ,
,
 ,
,
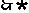
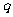 :
: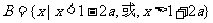 (8分)
(8分)
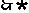
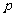 是
是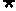
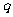 的必要不充分条件,
的必要不充分条件,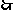
 的真子集 (10分)
的真子集 (10分)
 , (13分)
, (13分)
 (14分)
(14分)
11.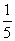 ;
12.
;
12.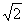 ;
; 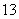 .
.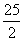 ; 14.9; 15.70;
16.0.3;
17.
; 14.9; 15.70;
16.0.3;
17.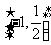
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com