7．若0<x≤2则函数y＝－x²+x+2的值域是________．

[解析]　y＝－x²+x+2＝－(x－)²+在(0,2]的图象．知f(x)在(0，]上是增函数，在[，2]上是减函数，所以y∈[0，]．

[答案]　[0，]

6．(2008·广州二模)设函数f(x)＝g(x)＝x²f(x－1)，则函数g(x)的递减区间是

(　)

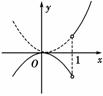
A．(－∞，0]　 　　　　　　　　　　　　 B．[0,1)

C．[1，+∞)　 　　　　　　　　　　　　 D．[－1,0]

[解析]　g(x)＝如右图所示，其递减区间是[0,1)．故选B.

[答案]　B

5．函数y＝1－ 的单调增区间是

(　)

A.　 　　　　　　　　　　　 B.

C．(－∞，1)　 　　　　　　　　　　　　 D．(2，+∞)

[解析]　由x²－3x+2≥0得x≤1或x≥2，要求原函数的递增区间，只需求t＝x²－3x+2的递减区间，即(－∞，1)，故选C.

[答案]　C

4．(2008·广州一模)函数y＝(0＜|x|≤1)的值域是

(　)

A．(－∞，－8]∪[0，+∞)　 　 B．[0，+∞)

C．[0,1]　 　　　　　　　　　　　　　　　　 D．(0,1]

[解析]　解法一：y＝

＝(x+2)+－4，

∵0＜|x|≤1，∴x+2∈[1,2)∪(2,3]，

又∵函数g(t)＝t+－4在[1,2)上是减函数，在(2,3]上是增函数，∴原函数的值域是(0,1]，故选D.

解法二：∵y′＝＝，

∴函数y＝在[－1,0)上是减函数，在(0,1]上是增函数．

∴原函数的值域为(0,1]∪(0，]＝(0,1]．

[答案]　D

3．(2007·福建)已知f(x)是R上的减函数，则满足

f>f(1)的实数x的取值范围是

(　)

A．(－∞，1)　 　　　　　　　　　　　　 B．(1，+∞)

C．(－∞，0)∪(0,1)　 　　　　　　　 D．(－∞，0)∪(1，+∞)

[解析]　由f(x)在R上是减函数，所以<1，解得x>1，或x<0，故选D.

[答案]　D

2. (2006·陕西)函数f(x)＝(x∈R)的值域是

(　)

A．(0,1)　 　　　　　　　　　　　　　　　　 B．(0,1]

C．[0,1)　 　　　　　　　　　　　　　　　　 D．[0,1]

[解析]　y＝x²+1≥1，

所以∈(0,1]．

故选B.

[答案]　B

1．(2009·福建)下列函数f(x)中，满足“对任意x₁，x₂∈(0，+∞)，当x₁＜x₂时，都有f(x₁)＞f(x₂)”的是

(　)

A．f(x)＝　 　　　　　　　　　　　　　　 B．f(x)＝(x－1)²

C．f(x)＝e^x　 　　　　　　　　　　　　　　　　　 D．f(x)＝ln(x+1)

[答案]　A

　　　 在世界环保日到来前夕,联合国教科文组织就如何处理城市垃圾向世界中学生征文。 请你以Saving Our City 为题, 写一篇100 字左右的短文。

提示:

　　　 城市垃圾的危害

　 (1)污染环境　　　

　 (2)有害健康

　　　 你所在的城市是如何处理垃圾的

　 (1)垃圾分类　 　

　 (2)报纸,玻璃的再利用

　 (3)有害垃圾填埋

　　　 此题要求改正所给短文中的错误。对标有题号的每一行作出判断： 如无错误，在该行右边横线上画一个勾( √ )；如有错误(每行只有一个错误)，则按下列情况改正：

　　　 此行多一个词： 把多余的词用斜线()划掉，在该行右边横线上写出该词，并也用斜线划掉。

　此行缺一个词： 在缺词处加一个漏字符号(∧)，在该行右边横线上写出该加的词。

　此行错一个词： 在错的词下划一横线，在该行右边横线上写出改正后的词。

　注意： 原行没有错的不要改。

　After I finished the school this year, I began 　　　71．__________

　to look for work．Now several month later, I still　　　72．__________

　hadn‘t found the job that I was interested．Last Sunday　 73．__________

　morning I received a phone call from a man calling him 　74．__________

　Mr Smith．He said to me on the phone, "I hear that you do 　75．__________

　very well in your studies．I may have a job for you．"　 　　76．__________

　I entered his office with a beaten heart．How I hoped　　77．__________

　that I will go through the job-hunting talk today and he　 　78．___________

　would take me on as a lab assistant．But to my surprised, 　79___________

　what he said disappointing．He only needed a model．　　80．___________