1.(08海南卷)白磷与氧可发生如下反应：P₄+5O₂=P₄O₁₀。已知断裂下列化学键需要吸收的能量分别为：P-P　 akJ·mol^-1、P-O bkJ·mol^-1、P=O ckJ·mol^-1、O=O　 dkJ·mol^-1。

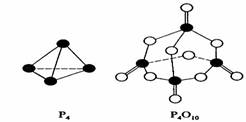
根据图示的分子结构和有关数据估算该反应的△H，其中正确的是　　　　 (　 )

A．(6a+5d－4c－12b)kJ·mol^-1 　　　　B(4c+12b－6a－5d)kJ·mol^-1

C．(4c+12b－4a－5d)kJ·mol^-1 D．(4a+5d－4c－12b)kJ·mol^-1

[答案]A

[解析]由图可以看出：P₄中有6mol的P－P，5mol的O₂中含有5molO＝O，1mol的P₄O₁₀中含有4mol的P＝O，12mol的P－O，所以△H＝(6a+5d－4c－12b)kJ·mol^－1。

[考点分析]化学反应热的有关计算

4. 计算反应热的规范书写：

(1)设未知量，写方程式，列比例式，求解，答。

(2)必须代数据，且数据后必须带单位。

(3)热化学方程式必须标明每种物质的聚集状态。

(4)注意正负号：放热反应的△H必然为负，但题目要求放出的热量时，放出的热量必须为正！

(5)△H为对应于某一特定反应的反应热，而不是某种物质的反应热，因此不能在△H后用下标或加括号代表某种物质的反应热！

(6)不能出现“3molC₂H₂的燃烧热”类似的表述！

(7)热化学方程式的加减用数字代表即可，不需要写出中间方程式。

[典例精析]

3. 混合物的计算　　　 十字交叉法

极限分析法

　　　　　　　　　　　　　 平均值法

估算法

2. 多步反应的计算：运用盖斯定律将热化学方程式(包括△H)进行加或减，得到新的热化学方程式后，再列比例关系式。

　　　　　　　　　　　　　 方程组法

1. 单一反应的计算：根据热化学方程式的数据列比例关系式。

12．(2007·上海)已知函数f(x)＝x²+(x≠0，a∈R)

(1)判断函数f(x)的奇偶性；

(2)若f(x)在区间[2，+∞)是增函数，求实数a的取值范围．

[解]　(1)当a＝0时，f(x)＝x²，

对任意x∈(－∞，0)∪(0，+∞)，f(－x)＝(－x)²＝x²＝f(x)，∴f(x)为偶函数．

当a≠0时，f(x)＝x²+(a≠0，x≠0)，

取x＝±1，得f(－1)+f(1)＝2≠0，

f(－1)－f(1)＝－2a≠0，

∴f(－1)≠－f(1)，f(－1)≠f(1)，

∴函数f(x)既不是奇函数，也不是偶函数．

(2)解法一：设x₂>x₁≥2，f(x₁)－f(x₂)＝x+－x－＝[x₁x₂(x₁+x₂)－a]，

由x₂≥x₁≥2得x₁x₂(x₁+x₂)>16，x₁－x₂<0，x₁x₂>0

要使f(x)在区间[2，+∞)是增函数只需f(x₁)－f(x₂)<0，

即x₁x₂(x₁+x₂)－a>0恒成立，则a≤16.

解法二：(导数法)，f′(x)＝2x－，要使f(x)在区间[2，+∞)是增函数，只需当x≥2时，f′(x)≥0恒成立，即2x－≥0，

则a≤2x³∈[16，+∞)恒成立，故当a≤16时，f(x)在区间[2，+∞)是增函数．

亲爱的同学请写上你的学习心得

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

________________________________________________________________________

11．已知函数f(x)＝ax²+2ax+1.x∈[－3,2]的最大值为4.求其最小值．

[解]　当a＝0时，f(x)＝1与已知不符．

当a≠0时，f(x)的图象为对称轴是x＝－1的抛物线上的一段．

当a<0时，4＝f(－1)＝－a+1.

∴a＝－3，

此时最小值为f(2)＝－23.

当a>0时，4＝f(2)＝8a+1，∴a＝，此时最小值为f(－1)＝.

10．若函数f(x)＝的值域为[0，+∞)，则实数a的取值范围是________．

[答案]　(－∞，－1]∪[0，+∞)

9．函数f(x)＝的最大值是________．

[解析]　∵1－x(1－x)＝1－x+x²＝(x－)²+≥，

∴f(x)＝≤.

[答案]　

8．如果函数f(x)＝x²+2(a－1)x+2在区间(－∞，4]上是减函数，则实数a的取值范围是________．

[解析]　∵f(x)＝x²+2(a－1)x+2，

∴对称轴为x＝1－a，∴递减区间为(－∞，1－a]

依题意，有(－∞，4)⊆(－∞，1－a]，

∴4≤1－a，得a≤－3.

[答案]　(－∞，－3]