
3.在正方形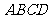 内任取一点
内任取一点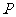 ,求
,求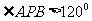 的概率.
的概率.
2.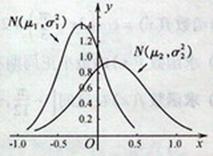 设两个正态分布
设两个正态分布 和
和
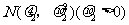 的密度函数图像如图所示。则有( )
的密度函数图像如图所示。则有( )
A.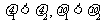 B.
B.
C.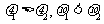 D.
D.
1. 12名同学合影,站成前排4人后排8人,现摄影师要从后排8人中抽2人调整到前排,若其他人的相对顺序不变,则不同调整方法的总数是( )
A.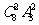 B.
B.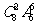 C.
C.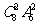 D.
D.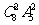
7.正态分布
例7.2009全国卷Ⅱ文)(本小题满分12分)某车间甲组有10名工人,其中有4名女工人;
乙组有10名工人,其中有6名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核。
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率。
解析 本题考查概率统计知识,要求有正确理解分层抽样的方法及利用分类原理处理事件概率的能力,第一问直接利用分层统计原理即可得人数,第二问注意要用组合公式得出概率,第三问关键是理解清楚题意以及恰有2名男工人的具体含义,从而正确分类求概率.
解 (1)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽
取4名工人进行技术考核,则从每组各抽取2名工人.
(2)记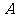 表示事件:从甲组抽取的工人中恰有1名女工人,则
表示事件:从甲组抽取的工人中恰有1名女工人,则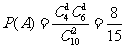
(3)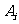 表示事件:从甲组抽取的2名工人中恰有
表示事件:从甲组抽取的2名工人中恰有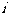 名男工人,
名男工人,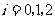
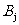 表示事件:从乙组抽取的2名工人中恰有
表示事件:从乙组抽取的2名工人中恰有 名男工人,
名男工人,
 表示事件:抽取的4名工人中恰有2名男工人。
表示事件:抽取的4名工人中恰有2名男工人。
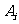 与
与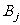 独立,
独立,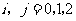 ,且
,且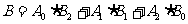
故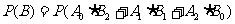
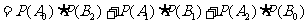
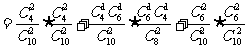
[专题突破]
6.随机变量的方差
例6.甲、乙两名工人加工同一种零件,两人每天加工的零件数相等,所得次品数分别为ε、η,ε和η的分布列如下:
|
ε |
0 |
1 |
2 |
η |
0 |
1 |
2 |
|
P |
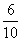 |
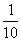 |
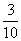 |
P |
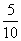 |
 |
 |
试对这两名工人的技术水平进行比较。
分析:一是要比较两名工人在加工零件数相等的条件下出次品数的平均值,即期望;二是要看出次品数的波动情况,即方差值的大小。
解析:工人甲生产出次品数ε的期望和方差分别为:
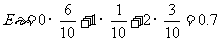 ,
,
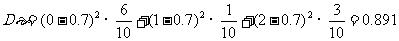 ;
;
工人乙生产出次品数η的期望和方差分别为:
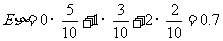 ,
,
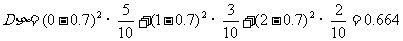 ;
;
由Eε=Eη知,两人出次品的平均数相同,技术水平相当,但Dε>Dη,可见乙的技术比较稳定。
5.随机变量的均值
例5.(1)(2009湖南卷文) 一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为10的样本.已知B层中每个个体被抽到的概率都为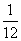 ,则总体中的个体数为 .
,则总体中的个体数为 .
答案 120
解析 设总体中的个体数为 ,则
,则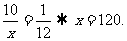

(2)(2009四川卷文)设矩形的长为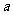 ,宽为
,宽为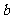 ,其比满足
,其比满足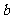 ∶
∶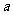 =
=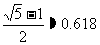 ,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
,这种矩形给人以美感,称为黄金矩形。黄金矩形常应用于工艺品设计中。下面是某工艺品厂随机抽取两个批次的初加工矩形宽度与长度的比值样本:
甲批次:0.598 0.625 0.628 0.595 0.639
乙批次:0.618 0.613 0.592 0.622 0.620
根据上述两个样本来估计两个批次的总体平均数,与标准值0.618比较,正确结论是
A.甲批次的总体平均数与标准值更接近
B.乙批次的总体平均数与标准值更接近
C.两个批次总体平均数与标准值接近程度相同
D.两个批次总体平均数与标准值接近程度不能确定
答案 A
解析 甲批次的平均数为0.617,乙批次的平均数为0.613
4.随机变量的分布列
例4.(2009全国卷Ⅱ理)(本小题满分12分)某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(1)求从甲、乙两组各抽取的人数; 
(I2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)记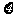 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求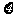 的分布列及数学期望。
的分布列及数学期望。

分析 (1)这一问较简单,关键是把握题意,理解分层抽样的原理即可。另外要注意
此分层抽样与性别无关。
(2)在第一问的基础上,这一问处理起来也并不困难。

从甲组抽取的工人中恰有1名女工人的概率

(3)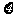 的可能取值为0,1,2,3
的可能取值为0,1,2,3
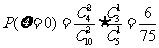 ,
,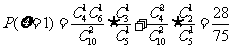 ,
,
 ,
,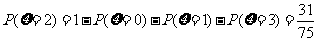

分布列及期望略. 
3.独立的概念及应用
例3.(2009山东卷理)某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的 
产品净重(单位:克)数据绘制的频率分布直方图,其中产品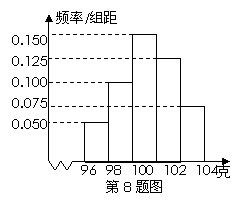

净重的范围是[96,106],样本数据分组为[96,98),[98,100),
[100,102),[102,104),[104,106],已知样本中产品净重小于
100克的个数是36,则样本中净重大于或等于98克并且
小于104克的产品的个数是
( ).
A.90
B.75
C. 60
D.45
答案 A
解析 产品净重小于100克的概率为(0.050+0.100)×2=0.300, 
已知样本中产品净重小于100克的个数是36,设样本容量为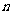 ,
,
则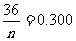 ,所以
,所以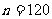 ,净重大于或等于98克并且小于
,净重大于或等于98克并且小于
104克的产品的概率为(0.100+0.150+0.125)×2=0.75,所以样本
中净重大于或等于98克并且小于104克的产品的个数是
120×0.75=90.故选A.
2.独立性检验
例2.为了探究患慢性气管炎是否与吸烟有关,调查了339名50岁以上的人,调查结果如下表所示:

|
|
患慢性气管炎 |
未患慢性气管炎 |
合计 |
|
吸烟 |
43 |
162 |
205 |
|
不吸烟 |
13 |
121 |
134 |
|
合计 |
56 |
283 |
339 |
试问:50岁以上的人患慢性气管炎与吸烟习惯有关吗?
解析:由公式 ,因为7.469>6.635,所以我们有99%的把握说:50岁以上的人患慢性气管炎与吸烟习惯有关。
,因为7.469>6.635,所以我们有99%的把握说:50岁以上的人患慢性气管炎与吸烟习惯有关。
1.线性相关性检验
例1.一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间由如下一组数据:
|
x |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
1.80 |
1.87 |
1.98 |
2.07 |
|
|
y |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
3.14 |
3.26 |
3.36 |
3.50 |
|
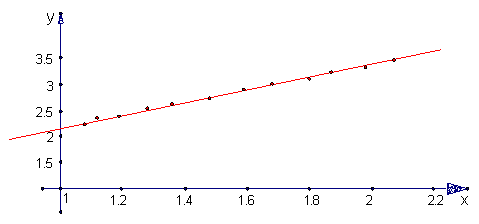
1)画出散点图;2)检验相关系数r的显著性水平;3)求月总成本y与月产量x之间的回归直线方程. 
解析:
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
xi |
1.08 |
1.12 |
1.19 |
1.28 |
1.36 |
1.48 |
1.59 |
1.68 |
1.80 |
1.87 |
1.98 |
2.07 |
|
yi |
2.25 |
2.37 |
2.40 |
2.55 |
2.64 |
2.75 |
2.92 |
3.03 |
3.14 |
3.26 |
3.36 |
3.50 |
|
xiyi |
2.43 |
2.264 |
2.856 |
3.264 |
3.590 |
4.07 |
4.643 |
5.090 |
5.652 |
6.096 |
6.653 |
7.245 |
 = =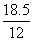 , ,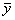 = =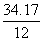 =2.8475, =2.8475, =29.808, =29.808,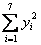 =99.2081, =99.2081, =54.243 =54.243 |
1)画出散点图:
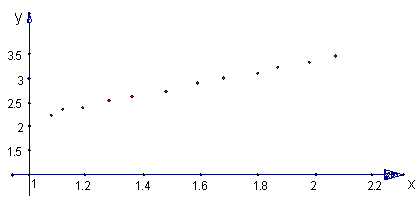

2)
r=

=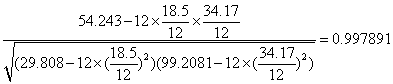

在“相关系数检验的临界值表”查出与显著性水平0.05及自由度12-2=10相应的相关数临界值r0.05=0.576<0.997891, 这说明每月产品的总成本y(万元)与该月产量x(万件)之间存在线性相关关系。
3)设回归直线方程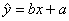 ,
,
利用
 ,
,
计算a,b,得b≈1.215,
a=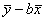 ≈0.974,
≈0.974,
∴回归直线方程为: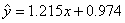


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com