
8、答:{1,2,3};解析:分析条件 同时为假命题,
同时为假命题,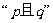 可化为
可化为 且
且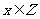 ,即不小于4的整数,或者不大于0的整数,因此
,即不小于4的整数,或者不大于0的整数,因此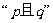 为假命题可化为
为假命题可化为 或者大于4的非整数及小于0的非整数;
或者大于4的非整数及小于0的非整数; 是假命题即为
是假命题即为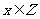 。因此
。因此 同时为假命题,是指满足
同时为假命题,是指满足 的整数。
的整数。
7、答案:充分不必要;解析:条件P化简为 ,命题Q化简为
,命题Q化简为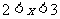
6、答: ;解析:注意利用“增函数”这个函数性质的功能,把函数值的大小关系转化为对应自变量的关系,由
;解析:注意利用“增函数”这个函数性质的功能,把函数值的大小关系转化为对应自变量的关系,由 得
得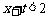 即
即 由
由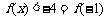 得
得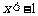 ,画数轴比较区间端点可得
,画数轴比较区间端点可得 得
得
5、答:
解析:化简 ,
, ,画数轴比较区间的端点可知条件转化为
,画数轴比较区间的端点可知条件转化为 ,求得
,求得
4、答:充分不必要;解析:首先理解原理: 所包含的条件意义为
所包含的条件意义为 是
是 成立充分条件,也说
成立充分条件,也说 是
是 成立的必要条件,化简两个集合
成立的必要条件,化简两个集合 ,
, 这里集合
这里集合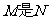 的真子集,因而命题
的真子集,因而命题 是
是 的充分不必要条件。
的充分不必要条件。
3、答:(1)(2)(4)
解析:此类命题的判断需注意各部分基础知识的运用,(1)中的角 终边相同或关于x轴对称;(2)中把相位
终边相同或关于x轴对称;(2)中把相位 看成一个整体,解
看成一个整体,解 得对称轴方程的一般形式为
得对称轴方程的一般形式为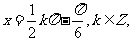 (4)中注意到
(4)中注意到 现象,偶函数而失去了周期性。
现象,偶函数而失去了周期性。
2、答: “ ”.解析:否命题是把原命题的条件和结论交换并且否定。
”.解析:否命题是把原命题的条件和结论交换并且否定。
1、答:1;解析:设 都是整数且
都是整数且 不可约,分别就正负与奇偶情况明确幂函数的单调性、奇偶性及图象所在限象,判断出原命题正确,可知它的逆否命题也正确;而其逆命题“若函数
不可约,分别就正负与奇偶情况明确幂函数的单调性、奇偶性及图象所在限象,判断出原命题正确,可知它的逆否命题也正确;而其逆命题“若函数 的图象不过第四象限,则函数
的图象不过第四象限,则函数 是幂函数”为假,故其否命题亦假。对于四种命题的真假判断,要充分利用原命题与其逆否命题等价,否命题与逆命题等价。
是幂函数”为假,故其否命题亦假。对于四种命题的真假判断,要充分利用原命题与其逆否命题等价,否命题与逆命题等价。
10、若命题“ ,使得
,使得 ”是真命题,则实数
”是真命题,则实数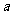 的取值范围是 .
的取值范围是 .
二 感悟解答
9、若命题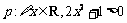 ,则该命题的否定是
,则该命题的否定是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com