1.从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同工作.若其中甲、乙两名志愿者都不能从事翻译工作,则选派方案共有　　　　 。

11. A,B,C,D,E五人站成一排:

(1)A,B两人相邻的不同排法有多少种?

(2)A,B,C两两不相邻的排法有多少种?

(3)A,B都与C相邻的不同排法种数有多少种?

(4)A,B,C顺序一定的排法有多少种

解:(1)将A,B两人看成一个元素,与C,D,E一起全排列,有种不同的排法, A,B有两种排列方法,共有2×24=48种不同的排法.

(2)A,B,C三人全排列有种不同的排法,D,E位于A与B,B与C之间,有2种排法,由乘法原理共有2×6=12种不同的排法.

(3)由已知可得A,B分别站在C的两端,有2种不同的站法,三人一起与D,E在全排列有,由乘法原理共有2×6=12种不同的排法.

(4)因A,B,C顺序一定,只需将D,E的位置找到并排好即可,有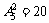种不同的排法.

10.用一颗骰子连掷三次,投掷出的数字顺次排成一个三位数,此时,

(1)　　 各位数字互不相同的三位数有多少个?

(2)　　 可以排出多少个不同的数?

解(1)第一个骰子有6种不同的结果,第二个骰子与第一个的结果不同,有5种不同的结果;同理第三个骰子有4种不同的结果,共有6×5×4=120个不同的结果.

(2)与(1)相比,后两个骰子都可以有6种不同的结果,共有个不同的结果.

9.= _________.

8.用数字1,2,3,4,5可以组成_________个没有重复数字且比13000大的正整数. 114

7.计划展出10幅不同的画,其中1幅水彩画,4幅油画,5幅国画,排成一行陈列,要求同一品种的画必须放在一起,并且水彩画不放在两端,不同的陈列种数有____种。5760

6.2个男生和4个女生排成一排,其中男生既不相邻也不排两端的不同排法共有____种。144

5.5名同学安排在星期一至星期五值日,每人一天,若甲同学不能排在星期一,乙同学不能排在星期五,则共有____种不同的值日方法。78

4.由数字0,1,2,3,4,5组成没有重复数字的六位数,其中偶数共有　　　　 　个。312

3.五名学生站成一排,其中甲必须站在乙的左边(可以不相邻)的站法种数为