

对一两句话或一段文字中的语句是否得体的考查试题,在解题时可用五看五审五改(客观题则只审辨不改正)法。
1.看对象,审尊卑长幼是否得体,改换谦敬词,做到谦敬词使用不错位。
用语简明,是达到运用语言高效的一个基本条件。简明,就是简要、明白。简要,表达同样的意思,用的语言要尽可能少,不用可有可无的字词,不重复哕嗦。明白,意思清楚明白,不致产生误解。
解答语言表达简明题,宜从两方面人手:
l.看语句(语段)中是否有意义相同、重复使用的词语,如果有,根据表意的实际情况,考虑这些重复是否必要,删去后能否影响表达效果或能否用其他的词语代换;注意修饰成分使用是否适当,有无滥用。
2.看语句(语段)在表意时,表意是否明确不产生歧义或不使人费解。消除歧义的方法有停顿消除法、重音消除法、变换词语法(包括单音词变双音词)、调序消除法、语境消除法等。
(二)择句归位题解题方法
 语意连贯的语段除了内容和逻辑的内在连贯外,还有表现形式上的连贯,即语言形式的结构美(结构形式大抵相同,字数大抵相等),这样的语句往往又具有对称美和韵律美。具有这“三美”的语段必然是连贯和和谐的。择句归位题就是设题人从一个句群(或语段)中间隔抽出一个或几个句子分别标上序号作选肢,要求考生填序号复位。
语意连贯的语段除了内容和逻辑的内在连贯外,还有表现形式上的连贯,即语言形式的结构美(结构形式大抵相同,字数大抵相等),这样的语句往往又具有对称美和韵律美。具有这“三美”的语段必然是连贯和和谐的。择句归位题就是设题人从一个句群(或语段)中间隔抽出一个或几个句子分别标上序号作选肢,要求考生填序号复位。
破解择句归位题要“三看一连”。三看,就是看结构、看对称、看韵律;一连,就是把结构相同或相似、字数大抵相等、具有对称美和韵律美的句子连在一起。下面例题的解析就用了这样的方法解题。
(一)主观排序题解题方法
1.通读文句,大体把握。
对题目所给的一组文句,作整体通读,求得两个大体把握:
①大体把握说什么,对所给文句组成的语段的话题有大体印象;
②大体把握怎么说,对所给文句组成的语段的层次有个大体印象。
2.根据印象,回头审视。
在通读文句获得总体印象的基础上,再回过头来,仔细审视文句,把能确定的东西确定下来。
如:沿着①的印象去审视,找出中心句。中心句一般在段首或段尾,根据该句子是领起句还是总结句进一步确定中心句的位置。沿着②的印象,一般能确定哪一个或几个句子是先说什么,哪一个或几个句子是接着说什么。走完这一步,比较简单的排序题便能得到准确答案。比较复杂的也能基本定下排序格局。
3.找过渡句,上挂下联。
如果经过l、2两个步骤还不能确定答案,排序比较复杂,则可用找过渡句、辨别关联词的方法,进一步审视。承上启下的过渡句考生不难找出,找出了过渡句,一个至多不过由7个句子组成的语段的脉络就基本清楚了。关联词的作用,是使上句和下旬相关相联。审视清楚含有关联词的句子之间的关系,就可以判定哪个分句应该在前,哪个分句应该在后。
4.先易后难,先分后合。
把一眼能看出其联系紧密,无疑应按先后放在一起的两个或两个以上的句子先组合成一个一个的小块,再审视这几个小块的逻辑条理,得出正确的排序。
表达连贯客观题有两种基本题型:主观排序题,择句归位题。
12.解析:∵AB=x, ∴AD=12-x.
又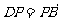 ,于是
,于是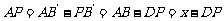 .
.
由勾股定理得 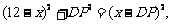 整理得
整理得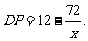
因此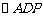 的面积
的面积 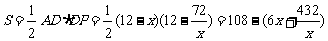 .
.
由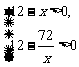 得
得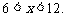
∴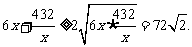 [来源:学.科.网]
[来源:学.科.网]
∴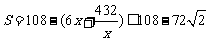 .
.
当且仅当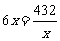 时,即当
时,即当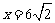
 时,S有最大值
时,S有最大值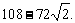
答:当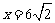 时,
时,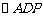 的面积有最大值
的面积有最大值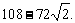
11.解析:(1)当a=-2,b=-8时,所给不等式左边=x2+ax+b|=|x2-2x-8|≤2|x2-2x-8|=|2x2-4x-16|=右边
∴此时所给不等式对一切x∈R成立
(2)注意到 2x2-4x-16=0 x2-2x-8=0
x2-2x-8=0 (x+2)(x-4)=0
(x+2)(x-4)=0 x=-2或x=4 ∴当x=-2或x=4时 |2x2-4x-16|=0
∴在不等式|x2+ax+b|≤|2x2-4x-16|中分
x=-2或x=4 ∴当x=-2或x=4时 |2x2-4x-16|=0
∴在不等式|x2+ax+b|≤|2x2-4x-16|中分 别取x=-2,x=4得
别取x=-2,x=4得 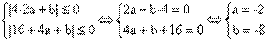 又注意到(1)知当a=-2,b=-8时,所给不等式互对一切x
又注意到(1)知当a=-2,b=-8时,所给不等式互对一切x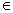 R均成立。∴满足题意
R均成立。∴满足题意 的实数a,b只能a=-2,b=-8一组
(3)由已知不等式x2-2x-8≥(m+2)x-m-15
的实数a,b只能a=-2,b=-8一组
(3)由已知不等式x2-2x-8≥(m+2)x-m-15
对一切x>2成立 x2-4x+7≥m(x-1)对一切x>2成立
x2-4x+7≥m(x-1)对一切x>2成立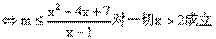 ①
令
①
令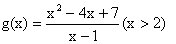 ② 则(1)
② 则(1) m≤g(x)的最小值
m≤g(x)的最小值
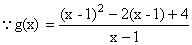
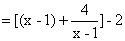 又当x>2时,x-1>0
又当x>2时,x-1>0
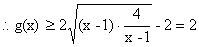 (当且仅当
(当且仅当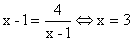 时等号成立)
∴g(x)的最小值为6(当且仅当x=3时取得) ③∴由②③得 m≤2 ∴所求实数m的取值范围为(-∞,2]
时等号成立)
∴g(x)的最小值为6(当且仅当x=3时取得) ③∴由②③得 m≤2 ∴所求实数m的取值范围为(-∞,2]
10.解析:(1)设矩形的另一边长为a m
则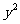 -45x-180(x-2)+180·2a=225x+360a-360
-45x-180(x-2)+180·2a=225x+360a-360
由已知xa=360,得a=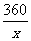 ,
,
所以y=2 25x+
25x+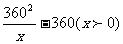 (II)
(II)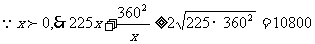
 .当且仅当225x=
.当且仅当225x=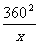 时,等号成立.
时,等号成立.
即当x=24m时,修建围墙的总费用最小,最小总费用是10440元.
9.解析: ,
,
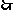 当且仅当
当且仅当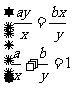 即
即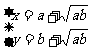 时,
时,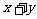 的最小值是
的最小值是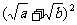 。
。
5.2-4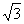 w.w.
w.w.

 w6.
w6.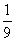 7.(1,3) 8.4
7.(1,3) 8.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com