
1、考字、词、句。某字、某词语的表达效果(作用),或赏析某句。
方法指导:这个字、词(或句)在诗中是什么的意思,这个字、词(或句)写出了人物或事物的什么样的特点特征、情况。表达了怎样的思想感情,有怎样的表达效果。
例1:09年四川卷
秋夜将晓出篱门迎凉有感(其二) 陆 游
三万里河东入海,五千仞岳上摩天。遗民泪尽胡尘里,南望王师又一年。
请谈谈这首诗前两句中“入”字和“摩”字的表达效果。(2分)
[答案] “入”字表现出河的生气,“摩”字突出了山的高峻。
例2:09年天津卷
严郑公宅同咏竹 唐·杜甫
绿竹半含箨,新梢才出墙。色侵书帙晚,阴过酒樽凉。
雨洗涓涓净,风吹细细香。但令无剪伐,会见拂云长。
请赏析“色侵书帙晚”一句。
[答案]翠竹的影子投映在书上,使人感到光线暗了下来。“侵”写出了竹影移动扩大的渐进过程。“晚”字则写出了竹影给人带来的时间错觉。
4、注意各种提示性信息,它们集中在题目、注释、诗中的某个词语--情点、题干要求等等。
针对诗歌鉴赏学习的规律,结合新课程改革对高考命题的指导性作用,积极探索高考新题型考查形式,探究不同考点的解题方法,做到有备无患。
探究解题方法
古典诗词鉴赏是高考语文试题的一项重要内容,重点考查对古诗词的鉴赏评价能力。《考纲》对此提出两项要求:一、鉴赏文学作品的形象,语言和表达技巧;二、评价文学作品的思想内容和作者的观点态度。自2002年始,高考诗歌鉴赏题主要采用了主观题的形式,试题灵活多变,异彩纷呈。考查的主要角度有:1、对词语、句子的理解,评价。2、对意象意境的鉴赏评析。3、对表现手法的辨析评价。4、对艺术风格,感情基调的评析。5、对内容主旨或思想感情的评析理解等。
结合2009年的试题题型,下面给大家提供几种常见的答题模式并附以题例,供参考。
3、弄清诗歌题材分类,体会作者思想感情,分析诗歌表现手法,如送别诗词,要注意诗歌感情是悲伤还是豁达乐观,作者是如何表现的,是否使用意象等。如田园诗歌,要理解作者在表达怎样的情趣等,这些都需要我们慎重思考。
2、形象的分类、语言鉴赏的命题形式、思想感情的表达模式、意境的种别、表达技巧题型等都要了解掌握。
1、明确鉴赏范围,并且要细化,因为诗歌鉴赏的命题点往往是从一首诗很小的一个方面来切入的。
基于上述分析,2010年备考复习应当针对高考动向,遵循学习规律。
遵循学习规律
作为毕业班语文教师,把握了高考动向,还要认真学习新课标的要求,了解新课标特点,探索每个考点的学习规律,从学生实际出发,指导教学。针对诗歌鉴赏题的特点,我们可以尝试遵循以下学习规律:
12.解析: (1)令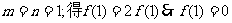
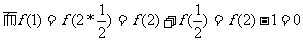
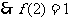 -----------
----------- ----------2’
----------2’
(2)设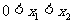 ,则
,则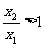 ,
,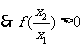

即
(3)由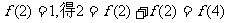 ,又
,又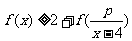
 --------------6’
--------------6’
又由(2)知,
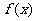 在
在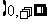 为单调递增函数
为单调递增函数
 --------------------------------------------7’
--------------------------------------------7’
1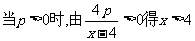

此时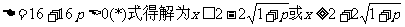
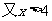
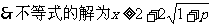 ------------9’
------------9’
2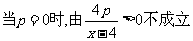 ,
,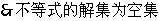 -----10’
-----10’
3当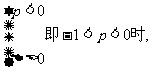
 [来源:]
[来源:]
 ,
,
解之得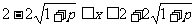 -------------------11’
-------------------11’
综上: 当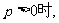 原不等式得解集为
原不等式得解集为
当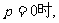 原不等式得解集为
原不等式得解集为
当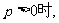 原不等式得解集为
原不等式得解集为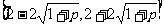 -----12’
-----12’
11.解析: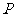 :
: 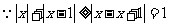
又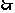 不等式
不等式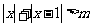 的解集为
的解集为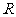
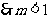
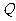 :
: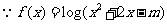 的定义域为
的定义域为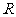
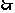 当
当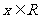 时
时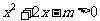 恒成立
恒成立
即 解得
解得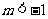

由题意知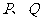 中恰有一个为真命题 即
中恰有一个为真命题 即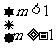 或
或 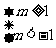 [来源:学+科+网]
[来源:学+科+网]
解得:
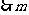 的取值范围为:
的取值范围为:
10.解析:(1)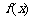 在
在 上是增函数,证明如下:
上是增函数,证明如下:
任取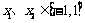 ,且
,且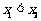 ,则
,则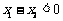 ,于是有
,于是有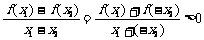 ,
,
而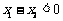 ,故
,故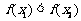 ,故
,故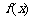 在
在 上是增函数
上是增函数
(2)由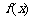 在
在 上是增函数知:
上是增函数知: 
 ,
,
故不等式的解集为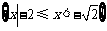 .
.
(3)由(1)知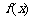 最大值为
最大值为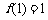 ,所以要使
,所以要使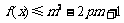 对所有的
对所有的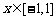 恒成立,
恒成立,
只需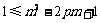 成立,即
成立,即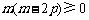 成立.
成立.
①
当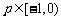 时,
时,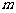 的取值范围为
的取值范围为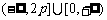 ;
;
②当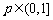 时,
时,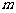 的取值范围为
的取值范围为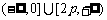 ;
;
③当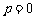 时,
时,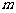 的取值范围为R.
的取值范围为R. 

9.解析:由(Ⅰ)真知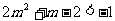
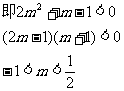
由(Ⅱ)真知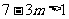
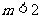
∴所以的取值范围是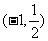
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com