
22.(本小题满分12分) 已知函数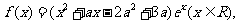 其中
其中 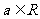
(1)当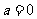 时,求曲线
时,求曲线 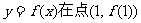 处的切线方程;
处的切线方程;
(2)当 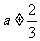 时,求函数
时,求函数
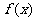 的单调区间与极值。
的单调区间与极值。
本小题主要考查导数的几何意义、导数的运算、利用导数研究函数的单调性与极值等基础知识,考查运算能力及分类讨论的思想方法。满分12分。
(I)解析
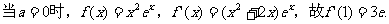
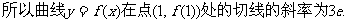
(II)
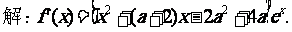
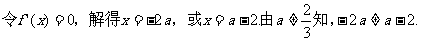
以下分两种情况讨论。
(1) >
>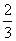 ,则
,则 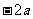 <
<
 .当 变化时,
.当 变化时,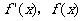 的变化情况如下表:
的变化情况如下表:
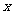

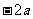
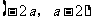

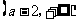
+ 0 - 0 +
↗ 极大值 ↘ 极小值 ↗

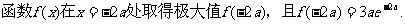
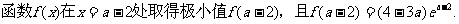

21. (本小题满分12分)已知向量m=(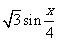 ,1),n=(
,1),n=(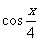 ,
,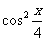 )。
)。
 (II)∵(2a-c)cosB=bcosC
(II)∵(2a-c)cosB=bcosC
由正弦定理得 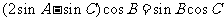
∴ 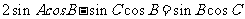
∴ 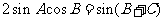
∵ 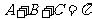
∴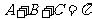 ,且
,且 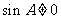
∴ 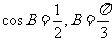
∴ 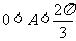
∴ 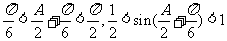
又∵f(x)=m•n=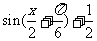 ,
,
∴f(A)=
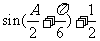 故函数f(A)的取值范围是(1,
故函数f(A)的取值范围是(1, 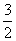 )
)
20.(本题满分12分)已知函数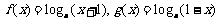 其中
其中 .
.
(1)求函数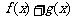 的定义域;
的定义域;
(2)求使
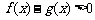 成立的
成立的
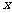 的集合.
的集合.
解答略
19.


18.(本题满分12分)为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 不喜爱打篮球 合计
男生 5
女生 10
合计 50
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 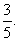
(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
下面的临界值表供参考:
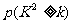 0.15 0.10 0.05 0.025 0.010 0.005 0.001
0.15 0.10 0.05 0.025 0.010 0.005 0.001
P 2.072 2.706 3.841 5.024 6.635 7.879 10.828
(参考公式: 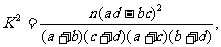 其中
其中
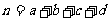 )
)
解:(Ⅰ)
列联表补充如下:
喜爱打篮球 不喜爱打篮球 合计
男生 20 5 25
女生 10 15 25
合计 30 20 50 ……6分
(Ⅱ) 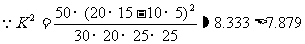 ……(10分)
……(10分)
的把握认为喜爱打篮球与性别有关。………………12分
17.(本题满分10分)已知 , 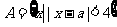 ,
,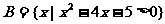 .
.
(I)若
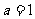 ,求
,求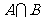 ;
;
(II)若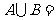 R,求实数
R,求实数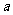 的取值范围.
的取值范围.
解 (I)当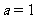 时,
时, 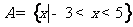 .
. 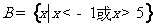
∴ 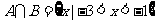
(II)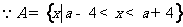 .
. 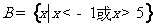 且
且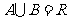
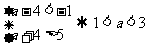 实数 的取值范围是
实数 的取值范围是 
22.(本小题满分12分)已知函数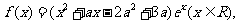 其中
其中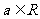
(1)当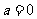 时,求曲线
时,求曲线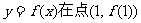 处的切线方程;
处的切线方程;
(2)当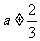 时,求函数
时,求函数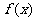 的单调区间与极值。
的单调区间与极值。
21. (本小题满分12分)已知向量m=(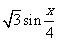 ,1),n=(
,1),n=(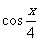 ,
,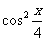 )。
)。
(1)若m•n=1,求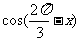 的值;
的值;
(2)记f(x)=m•n,在△ABC中,角A,B,C的对边分别是a,b,c,且满足(2a-c)cosB=bcosC,求函数f(A)的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com