
1、知识精讲:
1)当x→∞时函数f(x)的极限:
当自变量x取正值并且无限增大时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于正无穷大时, 函数f(x)的极限是a,记作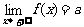 ,(或x→+∞时,f(x)→a)
,(或x→+∞时,f(x)→a)
当自变量x取负值并且无限增大时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于负无穷大时, 函数f(x)的极限是a,记作 ,(或x→-∞时,f(x)→a)
,(或x→-∞时,f(x)→a)
注:自变量x→+∞和x→-∞都是单方向的,而x→∞是双向的,故有以下等价命题




2)当x→x0时函数f(x)的极限:
当自变量x无限趋近于常数x0(但x≠x0)时,如果函数f(x)无限趋近于一个常数a,就说当x趋向于x0时, 函数f(x)的极限是a,记作 ,(或x→x0时,f(x)→a)
,(或x→x0时,f(x)→a)
注: 与函数f(x)在点x0处是否有定义及是否等于f(x0)都无关。
与函数f(x)在点x0处是否有定义及是否等于f(x0)都无关。
3)函数f(x)的左、右极限:
如果当x从点x=x0左侧(即x<x0)无限趋近于x0时,函数f(x)无限趋近于常数a。就说a是函数f(x)的左极限,记作 。
。
如果当x从点x=x0右侧(即x>x0)无限趋近于x0时,函数f(x)无限趋近于常数a。就说a是函数f(x)的右极限,记作 。
。
注:


 。并且可作为一个判断函数在一点处有无极限的重要工具。
。并且可作为一个判断函数在一点处有无极限的重要工具。
注:极限不存在的三种形态:①左极限不等于右极限
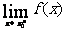 ;
;
② 时,
时,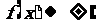 ,③
,③ 时,
时,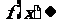 的值不唯一。
的值不唯一。
4)函数极限的运算法则:
与函数极限的运算法则类似, 如果 那么
那么




注:以上规则对于x→∞的情况仍然成立。
5.某个命题与正整数n有关,如果当 时命题成立,那么可推得当
时命题成立,那么可推得当 时命题也成立. 现已知当
时命题也成立. 现已知当 时该命题不成立,那么可推得(
C )
时该命题不成立,那么可推得(
C )
A.当n=6时该命题不成立 B.当n=6时该命题成立
C.当n=4时该命题不成立 D.当n=4时该命题成立
[典型例题选讲]
[例1]用数学归纳法证明下述等式问题:
(Ⅰ) .
.
[证明]
 . 当
. 当 时,左边
时,左边 ,右边
,右边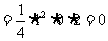 ,∴左边=右边,
,∴左边=右边, 时等式成立;
时等式成立;
 . 假设
. 假设 时等式成立,即
时等式成立,即
 ,
,
∴当 时,左边
时,左边


 =右边,即
=右边,即 时等式成立,
时等式成立,
根据 ,等式对
,等式对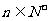 都正确.
都正确.
[例2]用数学归纳法证明下述整除问题:
(Ⅰ)求证: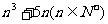 能被6 整除.
能被6 整除.
[证明]
 . 当
. 当 时,13+5×1=6能被6整除,命题正确;
时,13+5×1=6能被6整除,命题正确;
 . 假设
. 假设 时命题正确,即
时命题正确,即 能被6整除,
能被6整除,
∴当 时,
时,
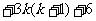 ,
,
∵两个连续的整数的乘积 是偶数,
是偶数, 能被6整除,
能被6整除,
 能被6整除,即当
能被6整除,即当 时命题也正确,
时命题也正确,
由 知命题时
知命题时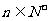 都正确.
都正确.
例3、(优化设计P202例1)比较2n与n2的大小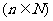
剖析:比较两数(或式)大小的常用方法本题不适用,故考虑用归纳法推测大小关系,再用数学归纳法证明.
解:当n=1时,21>12,
当n=2时,22=22,当n=3时,23<32,
当n=4时,24=42,当n=5时,25>52,
猜想:当n≥5时,2n>n2.
下面用数学归纳法证明:
(1)当n=5时,25>52成立.
(2)假设n=k(k∈N *,k≥5)时2k>k2,
那么2k+1=2·2k=2k+2k>k2+(1+1)k>k2+C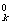 +C
+C +C
+C =k2+2k+1=(k+1) 2.
=k2+2k+1=(k+1) 2.
∴当n=k+1时,2n>n2.
由(1)(2)可知,对n≥5的一切自然数2n>n2都成立.
综上,得当n=1或n≥5时,2n>n2;当n=2,4时,2n=n2;当n=3时,2n<n2.
评述:用数学归纳法证不等式时,要恰当地凑出目标和凑出归纳假设,凑目标时可适当放缩.
例4、是否存在常数使 a、b、c 等式 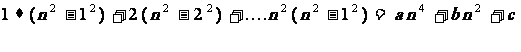 对一切正整数n成立?证明你的结论。
对一切正整数n成立?证明你的结论。
剖析:先取n=1,2,3探求a、b、c的值,然后用数学归纳法证明对一切n∈N*,a、b、c所确定的等式都成立.
解:分别用n=1,2,3代入解方程组

下面用数学归纳法证明.
(1)当n=1时,由上可知等式成立;
(2)假设当n=k+1时,等式成立,
则当n=k+1时,左边=1·[(k+1)2-12]+2[(k+1)2-22]+…+k[(k+1)2-k2]+(k+1)[(k+1)2-(k+1)2]=1·(k2-12)+2(k2-22)+…+k(k2-k2)+1·(2k+1)+2(2k+1)+…+k(2k+1)
= k4+(-
k4+(- )k2+(2k+1)+2(2k+1)+…+k(2k+1)=
)k2+(2k+1)+2(2k+1)+…+k(2k+1)= (k+1)4-
(k+1)4- (k+1)2.
(k+1)2.
∴当n=k+1时,等式成立.
由(1)(2)得等式对一切的n∈N*均成立.
评述:本题是探索性命题,它通过观察--归纳--猜想--证明这一完整的思路过程去探索和发现问题,并证明所得结论的正确性,这是非常重要的一种思维能力.
[例3](2003年全国)设a0为常数,且an=3n-1-2an-1(n∈N*).证明:n≥1时,an= [3n+(-1)n-1·2n]+(-1)n·2n·a0.
[3n+(-1)n-1·2n]+(-1)n·2n·a0.
剖析:给出了递推公式,证通项公式,可用数学归纳法证.
证明:(1)当n=1时, [3+2]-2a0=1-2a0,而a1=30-2a0=1-2a0.
[3+2]-2a0=1-2a0,而a1=30-2a0=1-2a0.
∴当n=1时,通项公式正确.
(2)假设n=k(k∈N*)时正确,即ak= [3k+(-1)k-1·2k]+(-1)k·2k·a0,
[3k+(-1)k-1·2k]+(-1)k·2k·a0,
那么ak+1=3k-2ak=3k- ×3k+
×3k+ (-1)k·2k+(-1)k+1·2k+1a0
(-1)k·2k+(-1)k+1·2k+1a0
=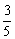 ·3k+
·3k+ (-1)k·2k+1+(-1)k+1·2k+1·a0
(-1)k·2k+1+(-1)k+1·2k+1·a0
= [3k+1+(-1)k·2k+1]+(-1)k+1·2k+1·a0.∴当n=k+1时,通项公式正确.
[3k+1+(-1)k·2k+1]+(-1)k+1·2k+1·a0.∴当n=k+1时,通项公式正确.
由(1)(2)可知,对n∈N*,an= [3n+(-1)n-1·2n]+(-1)n·2n·a0.
[3n+(-1)n-1·2n]+(-1)n·2n·a0.
评述:由n=k正确 n=k+1时也正确是证明的关键.
n=k+1时也正确是证明的关键.
例5、(优化设计P202例3) 设 为常数,且
为常数,且
证明对任意 ;
;
证法一:(i)当n=1时,由已知a1=1-2a0,等式成立;
(ii)假设当n=k(k≥1)等式成立,则
那么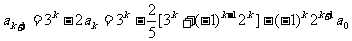

也就是说,当n=k+1时,等式也成立. 根据(i)和(ii),可知等式对任何n∈N,成立.
证法二:如果设 用
用 代入,可解出
代入,可解出 .
.
所以 是公比为-2,首项为
是公比为-2,首项为 的等比数列.
的等比数列.
 即
即
备用:平面内有n(n≥2)条直线,其中任何两条不平行,任何三条不过同一点,证明交点的个数为f(n)=  .
.
证明:(1)当n=2时,两条直线的交点只有一个,又f(2)= ×2×(2-1)=1,
×2×(2-1)=1,
因此,当n=2时,命题成立.
(2)假设当n=k(k≥2)时命题成立,就是说,平面内满足题设的任何k条直线的交点的个数f(k)等于 k(k-1).现在来考虑平面内有k+1条直线的情况.任取其中的一条直线,记为l.
k(k-1).现在来考虑平面内有k+1条直线的情况.任取其中的一条直线,记为l.
 (如例3图所示).由上述归纳法的假设,除l以外的其他k条直线的交点个数为f(k)=
(如例3图所示).由上述归纳法的假设,除l以外的其他k条直线的交点个数为f(k)= k(k-1).
k(k-1).
另外,因为已知任何两条直线不平行,所以直线l必与平面内其他k条直线都相交(有k个交点);又因为已知任何三条直线不过同一点,所以上面的k个交点两两不相同,且与平面内其他的 k·(k-1)个交点也两两不相同,从而平面内交点的个数是
k·(k-1)个交点也两两不相同,从而平面内交点的个数是 k(k-1)+k=
k(k-1)+k= k[(k-1)+2]=
k[(k-1)+2]= (k+1)[(k+1)-1].
(k+1)[(k+1)-1].
这就是说,当n=k+1时,k+1条直线的交点个数为
f(k+1)= (k+1)[(k+1)-1].
(k+1)[(k+1)-1].
根据(1)、(2)可知命题对任何大于1的正整数都成立.
[小结]
用数学归纳法证明恒等式的步骤及注意事项:明确首取值n0并验证真假(必不可少).“假设n=k时命题正确”并写出命题形式
分析“n=k+1时”命题是什么,并找出与“n=k”时命题形式的差别 弄清左端应增加的项
弄清左端应增加的项 明确等式左端变形目标,掌握恒等式变形常用的方法:乘法公式、因式分解、添拆项、配方等
明确等式左端变形目标,掌握恒等式变形常用的方法:乘法公式、因式分解、添拆项、配方等 可明确为:两个步骤、一个结论;递推基础不可少,归纳假设要用到,结论写明莫忘掉
可明确为:两个步骤、一个结论;递推基础不可少,归纳假设要用到,结论写明莫忘掉
[作业]教材闯关训练。
4.用数学归纳法证明“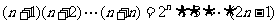 ”(
”(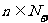 )时,从“
)时,从“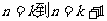 ”时,左边应增添的式子是 ( B )
”时,左边应增添的式子是 ( B )
A. B.
B. C.
C.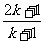 D.
D.
3.用数学归纳法证明 时,由
时,由 的假设到证明
的假设到证明 时,等式左边应添加的式子是( B )
时,等式左边应添加的式子是( B )
A. B.
B.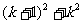 C.
C. D.
D.
2.设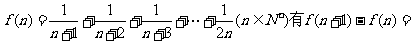 ,则
,则 ( D )
( D )
A. B.
B. C.
C. D.
D.
1.已知n为正偶数,用数学归纳法证明
 时,若已假设
时,若已假设 为偶数)时命题为真,则还需要用归纳假设再证 (B )
为偶数)时命题为真,则还需要用归纳假设再证 (B )
A. 时等式成立 B.
时等式成立 B. 时等式成立
时等式成立
C. 时等式成立 D.
时等式成立 D.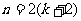 时等式成立
时等式成立
3.必须注意,数学归纳法不是对所有“与正整数n有关的命题”都有效.
基础题:
2.中学教材内,用数学归纳法证明的问题的主要题型有“等式问题”、“整除问题”、“不等式问题”等,要积累这几种题型的证题经验.
1.用数学归纳法证题要注意下面几点:
①证题的两个步骤缺一不可,要认真完成第一步的验证过程;
②成败的关键取决于第二步对 的证明:1)突破对“归纳假设”的运用;2)用好命题的条件;3)正确选择与命题有关的知识及变换技巧.
的证明:1)突破对“归纳假设”的运用;2)用好命题的条件;3)正确选择与命题有关的知识及变换技巧.
3.用数学归纳法证明一个与正整数有关的命题的步骤:
(1)证明:当n取第一个值n0结论正确;
(2)假设当n=k(k∈N*,且k≥n0)时结论正确,证明当n=k+1时结论也正确.
由(1),(2)可知,命题对于从n0开始的所有正整数n都正确
递推基础不可少,归纳假设要用到,结论写明莫忘掉 .
. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com