(三)例题与练习

例1、　 设集合A={1，3，a}，B={1，a2-a+1}

　　　 AÊB，求a的值

练习1：写出集合A={a，b，c}的所有子集，并指出哪些是真子集？有多少个？

例2 、 求满足{x|x²+2=0} 　MÍ{x|x2-1=0}的集合M.

例3、 若集合A={x|x²+x-6=0}，B={x|ax+1=0}

　　　 且B　　 A，求a的值.

练习2：　 集合M={x|x=1+a²，aÎN*}， P={x|x=a²-4a+5，aÎN*}

　　　　　 下列关系中正确的是(　 )

　　　　 A　 M　 P　　　 B　 P　 M　　　　

　　　　 C　 M=P　　　　 D　 M　 P　 且 P　 M

(三)“相等”关系

1、实例：设 A={x|x2-1=0}　 B={-1,1}　 　“元素相同”

结论：对于两个集合A与B，如果集合A的任何一个元素都是集合B的元素，同时,集合B的任何一个元素都是集合A的元素，我们就说集合A等于集合B，记作A=B(即如果AÍB　 同时 BÍA 那么A=B).

2、 ① 任何一个集合是它本身的子集.　 AÍA

② 真子集：如果AÍB ,且A¹B那就说集合A是集合B的真子集，记作A　 　B

③ 空集是任何非空集合的真子集.

④ 如果 AÍB, BÍC ,那么 AÍC.

　 证明：设x是A的任一元素，则 xÎA

　AÍB,xÎB　 　又 BÍC 　xÎC　 　从而　 AÍC　

同样；如果 AÍB, BÍC ,那么 AÍC

(二)空集的概念

不含任何元素的集合叫做空集，记作φ，并规定: 空集是任何集合的子集.

(一)子集的概念

1. 实例: A={1,2,3}　 B={1,2,3,4,5}　 引导观察.

　 结论: 对于两个集合A和B,如果集合A的任何一个元素都是集合B的元素,则说:这两个集合有包含关系，称集合A为集合B的子集，记作AÍB (或BÊA)，读作“A含于B”(或“B包含A”).

2. 反之: 集合A不包含于集合B,或集合B不包含集合A,记作AËB 已(或BËA)

3．关于“属于”的概念

2．集合的表示、符号、常用数集、列举法、描述法

1．集合的概念、集合三要素

集合的概念、表示；集合元素与集合间的关系；常用数集的记法.

(1)列举法：把集合中的元素一一列举出来,写在大括号内；

(2)描述法：用集合所含元素的共同特征表示的方法.(具体方法)

例 1、 用列举法表示下列集合：

(1)小于10的所有自然数组成的集合；

(2)方程x2=x的所有实数根组成的集合；

(3)由1~20以内的所有质数组成。

例 2、 试分别用列举法和描述法表示下列集合：

(1)由大于10小于20的的所有整数组成的集合；

(2)方程x2-2=2的所有实数根组成的集合.

注意：(1)描述法表示集合应注意集合的代表元素

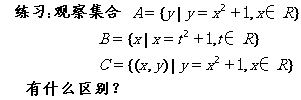(2)只要不引起误解集合的代表元素也可省略

　 非负整数集(或自然数集)，记作N；

　 除0的非负整数集，也称正整数集，记作N*或N+；

　 整数集，记作Z；

　 有理数集，记作Q； 　 实数集，记作R.

练习：(1)已知集合M={a，b，c}中的三个元素可构成某一三角形的三条边，那么此三角形一定不是(　　 )

　A直角三角形 　B 锐角三角形 　C钝角三角形　　 D等腰三角形

(2)说出集合{1，2}与集合{x=1，y=2}的异同点？