
本节主要学习了根式与分数指数幂以及指数幂的运算,分数指数幂是根式的另一种表示形式,根式与分数指数幂可以进行互化.在进行指数幂的运算时,一般地,化指数为正指数,化根式为分数指数幂,化小数为分数进行运算,便于进行乘除、乘方、开方运算,以达到化繁为简的目的,对含有指数式或根式的乘除运算,还要善于利用幂的运算法则.
(一)指数与指数幂的运算
1.根式的概念
一般地,如果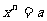 ,那么
,那么 叫做
叫做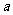 的
的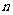 次方根(n th root),其中
次方根(n th root),其中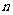 >1,且
>1,且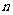 ∈
∈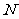 *.
*.
当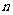 是奇数时,正数的
是奇数时,正数的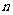 次方根是一个正数,负数的
次方根是一个正数,负数的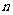 次方根是一个负数.此时,
次方根是一个负数.此时,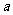 的
的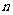 次方根用符号
次方根用符号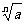 表示.
表示.
式子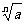 叫做根式(radical),这里
叫做根式(radical),这里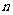 叫做根指数(radical exponent),
叫做根指数(radical exponent),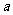 叫做被开方数(radicand).
叫做被开方数(radicand).
当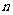 是偶数时,正数的
是偶数时,正数的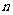 次方根有两个,这两个数互为相反数.此时,正数
次方根有两个,这两个数互为相反数.此时,正数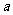 的正的
的正的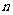 次方根用符号
次方根用符号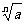 表示,负的
表示,负的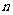 次方根用符号-
次方根用符号-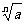 表示.正的
表示.正的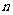 次方根与负的
次方根与负的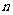 次方根可以合并成±
次方根可以合并成±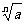 (
(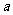 >0).
>0).
由此可得:负数没有偶次方根;0的任何次方根都是0,记作 .
.
思考:(课本P58探究问题)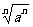 =
=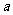 一定成立吗?.(学生活动)
一定成立吗?.(学生活动)
结论:当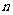 是奇数时,
是奇数时,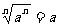
当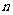 是偶数时,
是偶数时,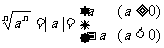
例1.(教材P58例1).
解:(略)
巩固练习:(教材P58例1)
2.分数指数幂
正数的分数指数幂的意义
规定:

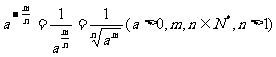
0的正分数指数幂等于0,0的负分数指数幂没有意义
指出:规定了分数指数幂的意义后,指数的概念就从整数指数推广到了有理数指数,那么整数指数幂的运算性质也同样可以推广到有理数指数幂.
3.有理指数幂的运算性质
(1) ·
·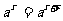
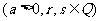 ;
;
(2)
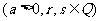 ;
;
(3)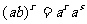
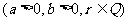 .
.
引导学生解决本课开头实例问题
例2.(教材P60例2、例3、例4、例5)
说明:让学生熟练掌握根式与分数指数幂的互化和有理指数幂的运算性质运用.
巩固练习:(教材P63练习1-3)
4. 无理指数幂
结合教材P62实例利用逼近的思想理解无理指数幂的意义.
指出:一般地,无理数指数幂 是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.
是一个确定的实数.有理数指数幂的运算性质同样适用于无理数指数幂.
思考:(教材P63练习4)
巩固练习思考::(教材P62思考题)
例3.(新题讲解)从盛满1升纯酒精的容器中倒出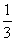 升,然后用水填满,再倒出
升,然后用水填满,再倒出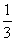 升,又用水填满,这样进行5次,则容器中剩下的纯酒精的升数为多少?
升,又用水填满,这样进行5次,则容器中剩下的纯酒精的升数为多少?
解:(略)
点评:本题还可以进一步推广,说明可以用指数的运算来解决生活中的实际问题.
4. 初中根式的概念;
如果一个数的平方等于a,那么这个数叫做a的平方根,如果一个数的立方等于a,那么这个数叫做a的立方根;
3. 复习初中整数指数幂的运算性质;

2. 由实例引入,了解指数指数概念提出的背景,体会引入指数的必要性;
1. 以折纸问题引入,激发学生的求知欲望和学习指数概念的积极性
3. 课后思考:
已知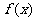 是定义在R上的函数,
是定义在R上的函数,
设 ,
,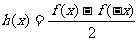
1 试判断 的奇偶性;
的奇偶性;
2 试判断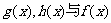 的关系;
的关系;
3 由此你能猜想得出什么样的结论,并说明理由.
2.补充作业:判断下列函数的奇偶性:
1 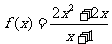 ;
;
2 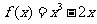 ;
;
3 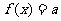 (
(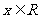 )
)
4 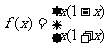
1. 书面作业:课本P46 习题1.3(A组) 第9、10题, B组第2题.
本节主要学习了函数的奇偶性,判断函数的奇偶性通常有两种方法,即定义法和图象法,用定义法判断函数的奇偶性时,必须注意首先判断函数的定义域是否关于原点对称.单调性与奇偶性的综合应用是本节的一个难点,需要学生结合函数的图象充分理解好单调性和奇偶性这两个性质.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com