
1. 对数的定义: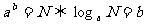 ;
;
教材P86习题2.2(A组) 第1、2题,(B组) 第1题.
1 引入对数的必要性;
2 指数与对数的关系;
3 对数的基本性质.
1.对数的概念
一般地,如果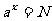
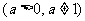 ,那么数
,那么数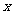 叫做以
叫做以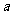 为底
为底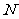 的对数(Logarithm),记作:
的对数(Logarithm),记作:
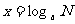
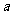 - 底数,
- 底数,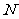 - 真数,
- 真数,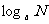 - 对数式
- 对数式
说明:1 注意底数的限制 ,且
,且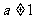 ;
;
 2
2 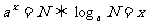 ;
;
3 注意对数的书写格式.
思考:1 为什么对数的定义中要求底数 ,且
,且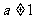 ;
;
2 是否是所有的实数都有对数呢?
设计意图:正确理解对数定义中底数的限制,为以后对数型函数定义域的确定作准备.
两个重要对数:
1 常用对数(common logarithm):以10为底的对数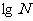 ;
;
2 自然对数(natural logarithm):以无理数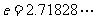 为底的对数的对数
为底的对数的对数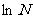 .
.
2. 尝试解决本小节开始提出的问题.
1. (对数的起源)价绍对数产生的历史背景与概念的形成过程,体会引入对数的必要性;
设计意图:激发学生学习对数的兴趣,培养对数学习的科学研究精神.
2. 选做题:教材P70习题2.1(B组) 第1题.
1. 必做题:教材P69习题2.1(A组) 第5、6、8、12题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com