
1.(知识方法准备)
1 学习指数函数时,对其性质研究了哪些内容,采取怎样的方法?
设计意图:结合指数函数,让学生熟知对于函数性质的研究内容,熟练研究函数性质的方法--借助图象研究性质.
2 对数的定义及其对底数的限制.
设计意图:为讲解对数函数时对底数的限制做准备.
3. 课外思考题:
设正整数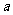 、
、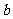 、
、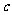 (
(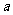 ≤
≤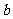 ≤
≤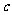 )和实数
)和实数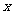 、
、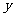 、
、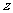 、
、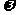 满足:
满足:
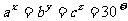 ,
, ,
,
求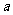 、
、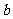 、
、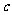 的值.
的值.
2. 提高题:
1 设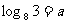 ,
,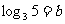 ,试用
,试用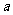 、
、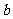 表示
表示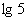 ;
;
2 设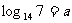 ,
,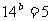 ,试用
,试用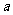 、
、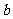 表示
表示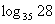 ;
;
3 设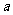 、
、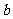 、
、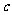 为正数,且
为正数,且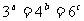 ,求证:
,求证: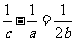 .
.
1. 基础题:教材P86习题2.2(A组) 第3 ~5、11题;
本节主要学习了对数的运算性质和换底公式的推导与应用,在教学中应用多给学生创造尝试、思考、交流、讨论、表达的机会,更应注重渗透转化的思想方法.
4. 课堂练习
1 教材P79练习4
2 已知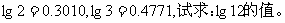
3 试求: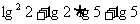 的值。(对换5与2,再试一试)
的值。(对换5与2,再试一试)
4 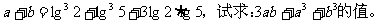
5 设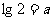 ,
,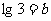 ,试用
,试用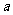 、
、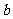 表示
表示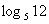
3. 换底公式
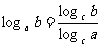 (
( ,且
,且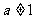 ;
;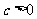 ,且
,且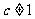 ;
;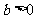 ).
).
学生活动
1 根据对数的定义推导对数的换底公式.
设计意图:了解换底公式的推导过程与思想方法,深刻理解指数与对数的关系.
2 思考完成教材P76问题(即本小节开始提出的问题);
3 利用换底公式推导下面的结论
(1)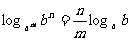 ;
;
(2)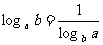 .
.
设计意图:进一步体会并熟练掌握换底公式的应用.
说明:利用换底公式解题时常常换成常用对数,但有时还要根据具体题目确定底数.
2. 利用科学计算器求常用对数和自然对数的值
设计意图:学会利用计算器、计算机求常用对数值和自然对数值的方法.
思考:对于本小节开始的问题中,可否利用计算器求解 的值?从而引入换底公式.
的值?从而引入换底公式.
2. 对数恒等式: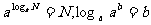 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com