1、知识与技能：(1)正确理解事件的包含、并事件、交事件、相等事件，以及互斥事件、对立事件的概念；

(2)概率的几个基本性质：1)必然事件概率为1，不可能事件概率为0，因此0≤P(A)≤1；2)当事件A与B互斥时，满足加法公式：P(A∪B)= P(A)+ P(B)；3)若事件A与B为对立事件，则A∪B为必然事件，所以P(A∪B)= P(A)+ P(B)=1，于是有P(A)=1-P(B)

(3)正确理解和事件与积事件，以及互斥事件与对立事件的区别与联系.

　　 复习二分法求解方程近似解的步骤

二分法是求方程近似解的一种常用方法，它是利用方程的根与对应的函数零点的关系，将求解方程转化为求解函数的零点的近似解。

(二)典型例题

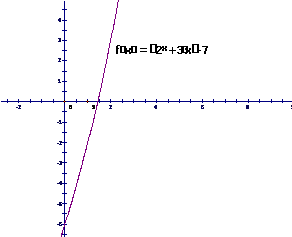
例2、借助电子计算器或计算机用二分法求方程2^x+3x=7的近似解(精确到0.1)

解：原方程即2^x+3x=7,令 f(x)=2^x+3x-7 ,用计算器或计算机作出函数f(x)=2^x+3x-7　 对应值表与图象(如下):

　　 由于　 |1.375-1.4375|=0.0625<0.1

　　 此时区间(1.375,1.4375)的两个端点精确到0.1的近似值都是1.4，所以原方程精确到0.1的近似解为1.4。

巩固练习：(教材P₁₀₆练习1)

(一)用二分法求方程的近似解

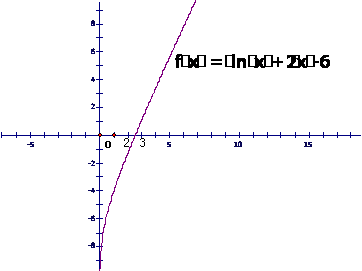
1．用二分法求方程Inx+2x-6=0的近似解

想法:如果能够将零点所在的范围尽量缩小,那么在一定精确度的要求下,我们可以得到零点的近似值.

一般地,我们把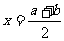 称为区间(a,b)的中点.

　　 2．二分法概念

　　 对于在区间[a,b]上连续不断、且f(a)*f(b)<0的函数y=f(x)，通过不断把函数f(x)的零点所在区间一分为二，使区间的两个端点逐步逼近零点，进而得到零点近似值的方法叫二分法

思考:

　　 　　　 为什么由|a-b|< ε,便可判断零点的的似值为a(或b)?

3、用二分法求方程的近似解的步骤

　　 ①、确定区间[a,b]，验证f(a)*f(b)<0，给定精确度ε

②、求区间(a,b)的中点x₁

③、计算f(x₁);

(1)　　 若f(x1)=0,则x1就是函数的零点

(2)　　 若f(x1)<0,则令b= x1(此时零点x0∈(a,x1))

(3)　　 若f(x1)>0,则令a= x1(此时零点x0∈(x1,b))

④、判断是否达到精确度ε，即若|a-b|< ε,则得到零点的近似值a(或b)；否则得复2-4

① 零点的概念:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点

② 连续函数在某个区间上存在零点的判别方法：

如果函数y=f(x)在区间[a,b]上的图象是连续不断一条曲线，并且有f(a)·f(b)<0，那么，函数y=f(x)在区间(a,b)内有零点.即存在c∈(a,b)，使得f(c )=0，这个c也就是方程f(x)=0的根.

　　 ③ 一元二次方程可以用公式求根,但没有公式来求Inx+2x-6=0的根.联系函数的零点与相应方程根的关系,能否利用函数的有关知识来求它的根呢？

7、作业：根据情况安排

5．解：天气预报的“降水”是一个随机事件，概率为90%指明了“降水”这个随机事件发生的概率，我们知道：在一次试验中，概率为90%的事件也可能不出现，因此，“昨天没有下雨”并不说明“昨天的降水概率为90%”的天气预报是错误的。

4．解：(1)填入表中的数据依次为0.75,0.8,0.8,0.85,0.83,0.8,0.76.(2)由于上述频率接近0.80，因此，进球的概率约为0.80。

3．解：(1)填入表中的数据依次为1,0.8,0.9,0.857,0.892,0.910,0.913,0.893,0.903,0.905.(2)该油菜子发芽的概率约为0.897。