2．过程与方法

(1)让学生通过直观感受空间物体，从实物中概括出柱、锥、台、球的几何结构特征。

(2)让学生观察、讨论、归纳、概括所学的知识。

1．知识与技能

(1)通过实物操作，增强学生的直观感知。

(2)能根据几何结构特征对空间物体进行分类。

(3)会用语言概述棱柱、棱锥、圆柱、圆锥、棱台、圆台、球的结构特征。

(4)会表示有关于几何体以及柱、锥、台的分类。

6．作业:

课本116页练习题集1、2题

5．小结

(1)解决实际问题的步骤：

实际问题　　 读懂问题　　 将问题抽象化　　 数学模型　　 解决问题

(2)几种常见函数的增长情况：

4．练习

某公司为了实现1000万元利润的目标，准备制定一个激励销售部门的奖励方案：在销售利润达到10万元时，按销售利润进行奖励，且资金y(单位：万元)随着销售利润x (单位：万元)的增加而增加，但资金数不超过5万元，同时奖金不超过利润的25%。现有三个奖励模型：y=0.25x，y=log7x+1，y=1.002x，其中哪个模型能符合公司的要求呢？

3．例题的启示：

解决实际问题的步骤：

(1)实际问题　　

(2)读懂问题抽象概括

(3)数学问题

(4)演算推理

(5)数学问题的解

(6)还原说明

(7)实际问题的解

2、例题

例1、假设你有一笔资金用于投资，现有三种投资方案供你选择，这三种方案的回报如下：

方案一：每天回报40元；

方案二：第一天回报10元，以后每天比前一天多 回报10元；

方案三：第一天回报0.4元，以后每天的回报比前一天翻一番。

请问，你会选择哪种投资方案呢？

投资方案选择原则：

投入资金相同，回报量多者为优

(1)　 比较三种方案每天回报量

(2) 比较三种方案一段时间内的总回报量

哪个方案在某段时间内的总回报量最多，我们就在那段时间选择该方案。

根据上表我们可以先建立三种投资方案所对应的函数模型，再通过比较它们的增长情况，为选择投资方案提供依据。

解：设第x天所得回报为y元，则　　　　　　

方案一：每天回报40元；　

　y=40　 (x∈N*)

方案二：第一天回报10元，以后每天比前一天多回 报10元；　　　　　　　　　　　　　　　　　　　 　　　 　　　　 y=10x (x∈N*)

方案三：第一天回报0.4元,以后每天的回报比前一天翻一番。

　　　　　 Y=0.4×2^x-1(x)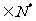

从每天的回报量来看：

第1~4天，方案一最多：　　　　　　　　　　　　　　　　　 　　　

每5~8天，方案二最多：　 　

第9天以后，方案三最多；　　　　　　　　　　　

　有人认为投资

1~4天选择方案一；

5~8天选择方案二；

9天以后选择方案三。

累积回报表

结论

投资8天以下(不含8天)，应选择第一种投资方案；投资8~10天，应选择第二种投资方案；投资11天(含11天)以上，应选择第三种投资方案。

1、　 背景

(1) 圆的周长随着圆的半径的增大而增大：

L=2πR　　　 (一次函数)

(2)圆的面积随着圆的半径的增大而增大：

S=πR²　　　 (二次函数)

(3)某种细胞分裂时，由1个分裂成两 个，两个分裂成4个……，一个这样的细

胞分裂x次后，得到的细胞个数y与x的函数关系是　　　 y = 2^x　 (指数 型函数)　　 。

运用计算机、实物投影仪等多媒体技术。

重点：将实际问题转化为函数模型，比教常数函数、一次函数、指数函数模型的增长差异；结合实例让学生体会直线上升，指数爆炸等不同函数型增长的函义。

　 难点：怎样选择数学模型分析解决实际问题。