
6.例题讲评
例1 设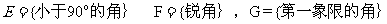 ,
,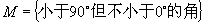 ,那么有( D
).
,那么有( D
).
A.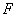
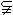
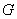
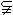
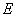 B.
B.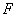
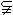
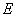
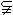
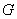 C.
C.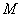
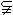 (
( 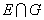 ) D.
) D.
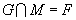
例2用集合表示:
(1)各象限的角组成的集合. (2)终边落在
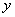 轴右侧的角的集合.
轴右侧的角的集合.
解:(1) 第一象限角:{α|k360oπ<α<k360o+90o,k∈Z}
第二象限角:{α|k360o+90o<α<k360o+180o,k∈Z}
第三象限角:{α|k360o+180o<α<k360o+270o,k∈Z}
第四象限角:{α|k360o+270o<α<k360o+360o ,k∈Z}
(2)在 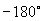 -
- 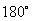 中,
中, 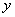 轴右侧的角可记为
轴右侧的角可记为 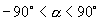 ,同样把该范围“旋转”
,同样把该范围“旋转” 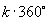 后,得
后,得 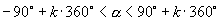 ,
, 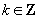 ,故
,故 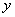 轴右侧角的集合为
轴右侧角的集合为 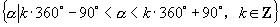 .
.
说明:一个角按顺、逆时针旋转
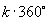 (
( 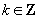 )后与原来角终边重合,同样一个“区间”内的角,按顺逆时针旋转
)后与原来角终边重合,同样一个“区间”内的角,按顺逆时针旋转 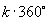 (
( 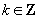 )角后,所得“区间”仍与原区间重叠.
)角后,所得“区间”仍与原区间重叠.
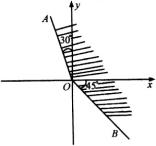 例3 (1)如图,终边落在
例3 (1)如图,终边落在 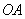 位置时的角的集合是__{α|α=k360o+120o ,k∈Z };终边落在
位置时的角的集合是__{α|α=k360o+120o ,k∈Z };终边落在 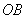 位置,且在
位置,且在 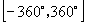 内的角的集合是_{-45o,225o}_ ;终边落在阴影部分(含边界)的角的集合
内的角的集合是_{-45o,225o}_ ;终边落在阴影部分(含边界)的角的集合
是_{α|k360o-45o<α<k360o+120o ,k∈Z}.
练习:
(1)请用集合表示下列各角.
①
 -
- 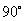 间的角 ②第一象限角 ③锐角 ④小于
间的角 ②第一象限角 ③锐角 ④小于 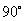 角.
角.
解答(1)① 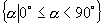 ; ②
; ②
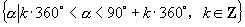 ;
;
③ 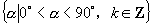 ; ④
; ④
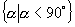
(2)分别写出:
①终边落在
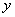 轴负半轴上的角的集合; ②终边落在
轴负半轴上的角的集合; ②终边落在 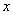 轴上的角的集合;
轴上的角的集合;
③终边落在第一、三象限角平分线上的角的集合;
④终边落在四象限角平分线上的角的集合.
解答(2)① 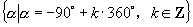 ; ②
; ②
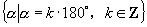 ;
;
③ 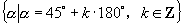 ; ④
; ④
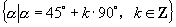 .
.
说明:第一象限角未必是锐角,小于
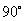 的角不一定是锐角,
的角不一定是锐角,  -
- 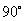 间的角,根据课本约定它包括
间的角,根据课本约定它包括  ,但不包含
,但不包含 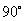 .
.
例4在 -
- 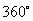 间,找出与下列各角终边相同的角,并判定它们是第几象限角
间,找出与下列各角终边相同的角,并判定它们是第几象限角
(1) 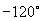 ;(2)
;(2)
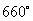 ;(3)
;(3)
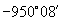 .
.
解:(1)∵ 
∴与 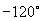 角终边相同的角是
角终边相同的角是
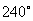 角,它是第三象限的角;
角,它是第三象限的角;
(2)∵ 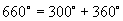
∴与 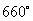 终边相同的角是
终边相同的角是
 ,它是第四象限的角;
,它是第四象限的角;
(3) 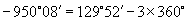
所以与 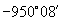 角终边相同的角是
角终边相同的角是
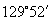 ,它是第二象限角.
,它是第二象限角.

总结:草式写在草稿纸上,正的角度除以
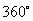 ,按通常除去进行;负的角度除以
,按通常除去进行;负的角度除以 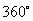 ,商是负数,它的绝对值应比被除数为其相反数时相应的商大1,以使余数为正值.
,商是负数,它的绝对值应比被除数为其相反数时相应的商大1,以使余数为正值.
练习:
(1)一角为 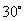 ,其终边按逆时针方向旋转三周后的角度数为_
,其终边按逆时针方向旋转三周后的角度数为_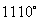 _.
_.
(2)集合M={α=k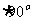 ,k∈Z}中,各角的终边都在(C )
,k∈Z}中,各角的终边都在(C )
A.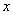 轴正半轴上, B.
轴正半轴上, B.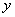 轴正半轴上,
轴正半轴上,
C. 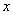 轴或
轴或 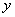 轴上, D.
轴上, D. 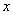 轴正半轴或
轴正半轴或 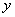 轴正半轴上
轴正半轴上
(3)设 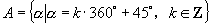 ,
, 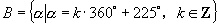
C={α|α= k180o+45o ,k∈Z} , 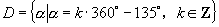

则相等的角集合为_B=D,C=E__.
5.终边相同的角的表示法
师:观察下列角你有什么发现? 390° -330° 30° 1470° -1770°
生:终边重合.
师:请同学们思考为什么?能否再举三个与300角同终边的角?
生:图中发现3900,-3300与300相差3600的整数倍,例如,3900=3600+300,-3300=-3600+300;与300角同终边的角还有7500,-6900等。
师:好!这位同学发现了两个同终边角的特征,即:终边相同的角相差3600的整数倍。例如:7500=2×3600+300;-6900=-2×3600+300。那么除了这些角之外,与300角终边相同的角还有:
3×3600+300 -3×3600+300
4×3600+300 -4×3600+300
……, ……,
由此,我们可以用S={β|β=k×3600+300,k∈Z}来表示所有与300角终边相同的角的集合。
师:那好,对于任意一个角α,与它终边相同的角的集合应如何表示?
生:S={β|β=α+k×3600,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和。
3.不是,一些特殊角终边可能落在坐标轴上;如果角的终边落在坐标轴上,就认为这个角不属于任一象限。
师:同学们一定要学会看数学书,特别是一些重要的概念、定理、性质要斟字酌句,每个字都要弄清楚,这样的预习才是有效果的。
师生讨论:好,按照象限角定义,图中的300,3900,-3300角,都是第一象限角;3000,-600角,都是第四象限角;5850角是第三象限角。
师:很好,不过老师还有几事不明,要请教大家:(1)锐角是第一象限角吗?第一象限角是锐角吗?为什么?
生:锐角是第一象限角,第一象限角不一定是锐角;
师:(2)锐角就是小于900的角吗?
生:小于900的角可能是零角或负角,故它不一定是锐角;
师:(3)锐角就是00-900的角吗?
生:锐角:{θ|00<θ<900};00-900的角:{θ|00≤θ<900}.
学生练习(口答) 已知角的顶点与坐标系原点重合,始边落在x轴的非负半轴上,作出下列各角,并指出它们是哪个象限的角?
(1)4200; (2)-750; (3)8550; (4)-5100.
答:(1)第一象限角;(2)第四象限角;(3)第二象限角;(4)第三象限角.
3.是不是任意角都可以归结为是象限角,为什么?
处理:学生思考片刻后回答,教师适时予以纠正。
答:1.不行,始边包括端点(原点); 2.端点在原点上;
2.定义中有个小括号,内容是:除端点外,请问课本为什么要加这四个字?
1.定义中说:角的始边与x轴的非负半轴重合,如果改为与x轴的正半轴重合行不行,为什么?
4.象限角
师:在今后的学习中,我们常在直角坐标系内讨论角,为此我们必须了解象限角这个概念。同学们已经经过预习,请一位同学回答什么叫:象限角?
生:角的顶点与原点重合,角的始边与x轴的非负半轴重合。那么,角的终边(除端点外)在第几象限,我们就说这个角是第几象限角。
师:很好,从刚才这位同学的回答可以知道,她已经基本理解了“象限角”的概念了。下面请大家将书上象限角的定义划好,同时思考这么三个问题:
3.正角、负角、零角概念
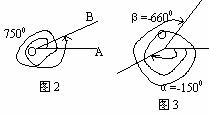
师:为了区别起见,我们把按逆时针方向旋转所形成的角叫正角,如图2中的角为正角,它等于300与7500;我们把按逆时针方向旋转所形成的角叫正角,那么同学们猜猜看,负角怎么规定呢?零角呢?
生:按顺时针方向旋转所形成的角叫负角,如果一条射线没有作任何旋转,我们称它形成了一个零角。
师:如图3,以OA为始边的角α=-1500,β=-6600。特别地,当一条射线没有作任何旋转时,我们也认为这是形成了一个角,并把这个角称为零角。
 师:好,角的概念经过这样的推广之后,就应该包括正角、负角、零角。这里还有一点要说明:为了简单起见,在不引起混淆的前提下,“角α”或“∠α”可简记为α.
师:好,角的概念经过这样的推广之后,就应该包括正角、负角、零角。这里还有一点要说明:为了简单起见,在不引起混淆的前提下,“角α”或“∠α”可简记为α.
2.角的概念的推广:
(1)定义:一条射线OA由原来的位置OA,绕着它的端点O按一定方向旋转到另一位置OB,就形成了角α。其中射线OA叫角α的始边,射线OB叫角α的终边,O叫角α的顶点。
1.回忆:初中是任何定义角的?
(从一个点出发引出的两条射线构成的几何图形)这种概念的优点是形象、直观、容易理解,但它的弊端在于“狭隘”
师:初中时,我们已学习了0○-360○角的概念,它是如何定义的呢?
 生:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形。
生:角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形。
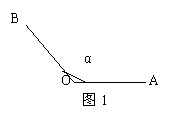
师:如图1,一条射线由原来的位置OA,绕着它的端点O按逆时针方向旋转到终止位置OB,就形成角α。旋转开始时的射线OA叫做角的始边,OB叫终边,射线的端点O叫做叫α的顶点。
师:在体操比赛中我们经常听到这样的术语:“转体720o” (即转体2周),“转体1080o”(即转体3周);再如时钟快了5分钟,现要校正,需将分针怎样旋转?如果慢了5分钟,又该如何校正?
生:逆时针旋转300;顺时针旋转300.
师:(1)用扳手拧螺母;(2)跳水运动员身体旋转.说明旋转第二周、第三周……,则形成了更大范围内的角,这些角显然超出了我们已有的认识范围。本节课将在已掌握
 -
- 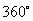 角的范围基础上,重新给出角的定义,并研究这些角的分类及记法.
角的范围基础上,重新给出角的定义,并研究这些角的分类及记法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com