
1.三角函数定义
在直角坐标系中,设α是一个任意角,α终边上任意一点 (除了原点)的坐标为
(除了原点)的坐标为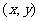 ,它与原点的距离为
,它与原点的距离为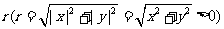 ,那么
,那么
(1)比值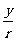 叫做α的正弦,记作
叫做α的正弦,记作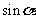 ,即
,即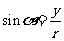 ;
;
(2)比值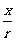 叫做α的余弦,记作
叫做α的余弦,记作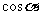 ,即
,即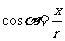 ;
;
(3)比值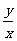 叫做α的正切,记作
叫做α的正切,记作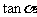 ,即
,即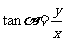 ;
;
(4)比值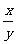 叫做α的余切,记作
叫做α的余切,记作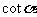 ,即
,即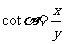 ;
;
(5)比值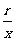 叫做α的正割,记作
叫做α的正割,记作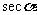 ,即
,即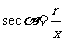 ;
;
(6)比值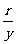 叫做α的余割,记作
叫做α的余割,记作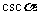 ,即
,即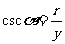 .
.
说明:①α的始边与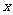 轴的非负半轴重合,α的终边没有表明α一定是正角或负角,以及α的大小,只表明与α的终边相同的角所在的位置;
轴的非负半轴重合,α的终边没有表明α一定是正角或负角,以及α的大小,只表明与α的终边相同的角所在的位置;
②根据相似三角形的知识,对于确定的角α,六个比值不以点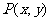 在α的终边上的位置的改变而改变大小;
在α的终边上的位置的改变而改变大小;
③当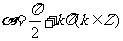 时,α的终边在
时,α的终边在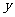 轴上,终边上任意一点的横坐标
轴上,终边上任意一点的横坐标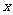 都等于
都等于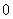 ,所以
,所以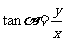 与
与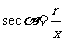 无意义;同理,当
无意义;同理,当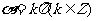 时,
时, 与
与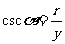 无意义;
无意义;
④除以上两种情况外,对于确定的值α,比值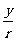 、
、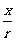 、
、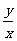 、
、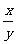 、
、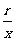 、
、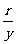 分别是一个确定的实数,所以正弦、余弦、正切、余切、正割、余割是以角为自变量,一比值为函数值的函数,以上六种函数统称为三角函数。
分别是一个确定的实数,所以正弦、余弦、正切、余切、正割、余割是以角为自变量,一比值为函数值的函数,以上六种函数统称为三角函数。
初中锐角的三角函数是如何定义的?
在Rt△ABC中,设A对边为a,B对边为b,C对边为c,锐角A的正弦、余弦、正切依次为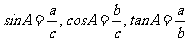 .
.
角推广后,这样的三角函数的定义不再适用,我们必须对三角函数重新定义。
(五)课外练习
1.自己动手制作一个底面是正方形,侧面是全等的三角形的棱锥模型,并画出它的三视图。
2.自己制作一个上、下底面都是相似的正三角形,侧面是全等的等腰梯形的棱台模型,并画出它的三视图。
(四)归纳整理
请学生回顾发表如何作好空间几何体的三视图
(三)巩固练习
课本P12 练习1、2 P18习题1.2 A组1
(二)实践动手作图
1.讲台上放球、长方体实物,要求学生画出它们的三视图,教师巡视,学生画完后可交流结果并讨论;
2.教师引导学生用类比方法画出简单组合体的三视图
(1)画出球放在长方体上的三视图
(2)画出矿泉水瓶(实物放在桌面上)的三视图
学生画完后,可把自己的作品展示并与同学交流,总结自己的作图心得。
作三视图之前应当细心观察,认识了它的基本结构特征后,再动手作图。
3.三视图与几何体之间的相互转化。
(1)投影出示图片(课本P10,图1.2-3)
请同学们思考图中的三视图表示的几何体是什么?
(2)你能画出圆台的三视图吗?
(3)三视图对于认识空间几何体有何作用?你有何体会?
教师巡视指导,解答学生在学习中遇到的困难,然后让学生发表对上述问题的看法。
4.请同学们画出1.2-4中其他物体表示的空间几何体的三视图,并与其他同学交流。
(一)创设情景,揭开课题
“横看成岭侧看成峰”,这说明从不同的角度看同一物体视觉的效果可能不同,要比较真实反映出物体,我们可从多角度观看物体,这堂课我们主要学习空间几何体的三视图。
在初中,我们已经学习了正方体、长方体、圆柱、圆锥、球的三视图(正视图、侧视图、俯视图),你能画出空间几何体的三视图吗?
2.教学用具:实物模型、三角板
1.学法:观察、动手实践、讨论、类比
重点:画出简单组合体的三视图
难点:识别三视图所表示的空间几何体
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com