
1.三角函数的定义及定义域、值域:
练习1:已知角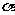 的终边上一点
的终边上一点 ,且
,且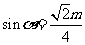 ,求
,求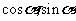 的值。
的值。
解:由题设知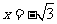 ,
,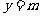 ,所以
,所以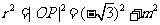 ,得
,得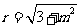 ,
,
从而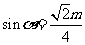
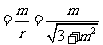 ,解得
,解得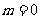 或
或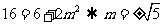 .
.
当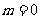 时,
时,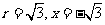 ,
,
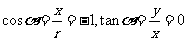 ;
;
当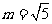 时,
时,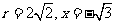 ,
,
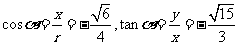 ;
;
当 时,
时,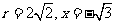 ,
,
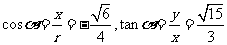 .
.
补充:1已知点
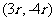
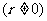 ,在角
,在角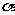 的终边上,求
的终边上,求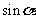 、
、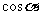 、
、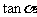 的值。
的值。
2已知角a的终边经过P(4,-3),求2sina+cosa的值
解:由定义 : sina=-
sina=-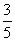 cosa=
cosa=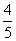 ∴2sina+cosa=-
∴2sina+cosa=-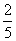
3.三角函数的符号及诱导公式。
2.三角函数的定义域、值域;
1.任意角的三角函数的定义;
1 确定下列三角函数值的符号:
(1)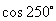 ; (2)
; (2)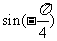 ; (3)
; (3)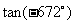 ; (4)
; (4)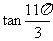 .
.
2 求函数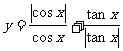 的值域
的值域
解: 定义域:cosx¹0 ∴x的终边不在x轴上
又∵tanx¹0 ∴x的终边不在y轴上
∴当x是第Ⅰ象限角时,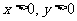 cosx=|cosx| tanx=|tanx| ∴y=2
cosx=|cosx| tanx=|tanx| ∴y=2
…………Ⅱ…………,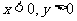 |cosx|=-cosx |tanx|=-tanx ∴y=-2
|cosx|=-cosx |tanx|=-tanx ∴y=-2
…………ⅢⅣ………, 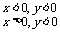 |cosx|=-cosx |tanx|=tanx ∴y=0
|cosx|=-cosx |tanx|=tanx ∴y=0
5.诱导公式
由三角函数的定义,就可知道:终边相同的角三角函数值相同。
即有:
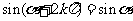 ,
,
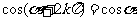 ,其中
,其中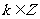 .
.
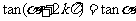 ,
,
这组公式的作用是可把任意角的三角函数值问题转化为0-2π间角的三角函数值问题.
4.三角函数的符号
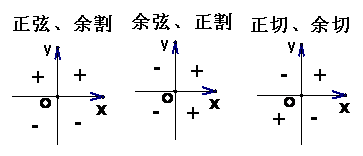
由三角函数的定义,以及各象限内点的坐标的符号,我们可以得知:
①正弦值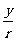 对于第一、二象限为正(
对于第一、二象限为正( ),对于第三、四象限为负(
),对于第三、四象限为负(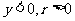 );
);
②余弦值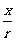 对于第一、四象限为正(
对于第一、四象限为正(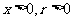 ),对于第二、三象限为负(
),对于第二、三象限为负(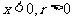 );
);
③正切值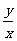 对于第一、三象限为正(
对于第一、三象限为正(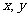 同号),对于第二、四象限为负(
同号),对于第二、四象限为负(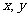 异号).
异号).
说明:若终边落在轴线上,则可用定义求出三角函数值。
 为正 全正
为正 全正
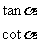 为正
为正 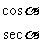 为正
为正
3.例题分析
例1.已知角α的终边经过点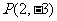 ,求α的六个函数制值。
,求α的六个函数制值。
解:因为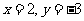 ,所以
,所以 ,于是
,于是
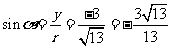 ;
;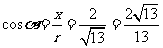 ;
;
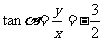 ;
;
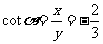 ;
;
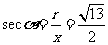 ;
;
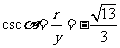 .
.
例2.求下列各角的六个三角函数值:
(1)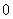 ;
(2)
;
(2)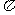 ;
(3)
;
(3)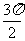 .
.
解:(1)因为当 时,
时,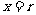 ,
,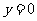 ,所以
,所以
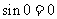 ,
,
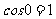 ,
,
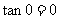 ,
,
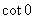 不存在,
不存在,
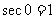 ,
,
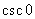 不存在。
不存在。
(2)因为当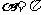 时,
时,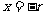 ,
,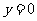 ,所以
,所以
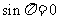 ,
,
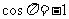 ,
,
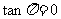 ,
,
 不存在,
不存在,
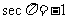 ,
, 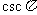 不存在。
不存在。
(3)因为当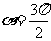 时,
时,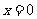 ,
,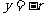 ,所以
,所以
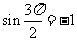 ,
,
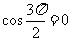 ,
,
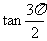 不存在,
不存在,
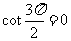 ,
,
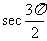 不存在,
不存在,
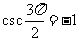 .
.
例3.已知角α的终边过点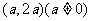 ,求α的六个三角函数值。
,求α的六个三角函数值。
解:因为过点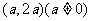 ,所以
,所以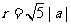 ,
, 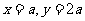
当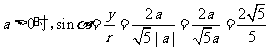 ;
;
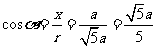 ;
;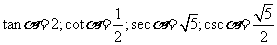 ;
;
当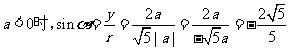 ;
;
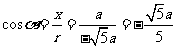 ;
;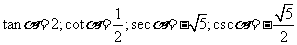 .
.
2.三角函数的定义域、值域
|
函 数 |
定 义 域 |
值 域 |
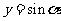 |
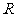 |
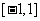 |
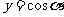 |
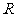 |
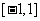 |
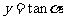 |
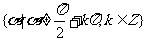 |
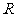 |
注意:
(1)以后我们在平面直角坐标系内研究角的问题,其顶点都在原点,始边都与x轴的非负半轴重合.
(2) α是任意角,射线OP是角α的终边,α的各三角函数值(或是否有意义)与ox转了几圈,按什么方向旋转到OP的位置无关.
(3)sin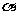 是个整体符号,不能认为是“sin”与“α”的积.其余五个符号也是这样.
是个整体符号,不能认为是“sin”与“α”的积.其余五个符号也是这样.
(4)任意角的三角函数的定义与锐角三角函数的定义的联系与区别:
锐角三角函数是任意角三角函数的一种特例,它们的基础共建立于相似(直角)三角形的性质,“r”同为正值. 所不同的是,锐角三角函数是以边的比来定义的,任意角的三角函数是以坐标与距离、坐标与坐标、距离与坐标的比来定义的,它也适合锐角三角函数的定义.实质上,由锐角三角函数的定义到任意角的三角函数的定义是由特殊到一般的认识和研究过程.
(5)为了便于记忆,我们可以利用两种三角函数定义的一致性,将直角三角形置于平面直角坐标系的第一象限,使一锐角顶点与原点重合,一直角边与x轴的非负半轴重合,利用我们熟悉的锐角三角函数类比记忆.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com