(四) 巩固深化、反馈矫正

⑴正方形的内切球和外接球的体积的比为　　　　　 ，表面积比为　　　　　 。

　　　　　　　　　　　　　　　　　　　　　　 (答案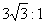：　 ；　3 ：1)

⑵在球心同侧有相距9cm的两个平行截面，它们的面积分别为49πcm²和400πcm²，求球的表面积。　 (答案：2500πcm²)

分析：可画出球的轴截面，利用球的截面性质求球的半径

(三) 典例分析

　 课本P₄₇ 例4和P₂₉例5

(二) 探究新知

1．球的体积：

如果用一组等距离的平面去切割球，当距离很小之时得到很多“小圆片”，“小圆片”的体积的体积之和正好是球的体积，由于“小圆片”近似于圆柱形状，所以它的体积也近似于圆柱形状，所以它的体积有也近似于相应的圆柱和体积，因此求球的体积可以按“分割--求和--化为准确和”的方法来进行。

步骤：

第一步：分割

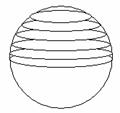　如图：把半球的垂直于底面的半径OA作n等分，过这些等分点，用一组平行于底面的平面把半球切割成n个“小圆片”，“小圆片”厚度近似为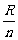，底面是“小圆片”的底面。

如图：

得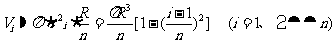

第二步：求和

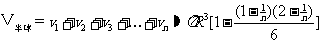
第三步：化为准确的和

　当n→∞时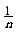， →0　 (同学们讨论得出)

所以　

得到定理：半径是R的球的体积

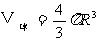
练习：一种空心钢球的质量是142g,外径是5cm,求它的内径(钢的密度是7.9g/cm³)

2．球的表面积：

球的表面积是球的表面大小的度量,它也是球半径R的函数,由于球面是不可展的曲面,所以不能像推导圆柱、圆锥的表面积公式那样推导球的表面积公式,所以仍然用“分割、求近似和，再由近似和转化为准确和”方法推导。

思考：推导过程是以什么量作为等量变换的？

　　　 半径为R的球的表面积为　　 S＝4πR²

　　 练习：长方体的一个顶点上三条棱长分别为3、4、5，是它的八个顶点都在同一球面上，则这个球的表面积是　　　　　 。 (答案50元)

(一) 创设情景

⑴教师提出问题：球既没有底面，也无法像在柱体、锥体和台体那样展开成平面图形，那么怎样来求球的表面积与体积呢？引导学生进行思考。

⑵教师设疑：球的大小是与球的半径有关，如何用球半径来表示球的体积和面积？激发学生推导球的体积和面积公式。

2．　 教学用具：投影仪

重点：引导学生了解推导球的体积和面积公式所运用的基本思想方法。

难点：推导体积和面积公式中空间想象能力的形成。

3．　 情感与价值观

　通过学习，使我们对球的体积和面积公式的推导方法有了一定的了解，提高了空间思维能力和空间想象能力，增强了我们探索问题和解决问题的信心。

2．　 过程与方法

通过球的体积和面积公式的推导，从而得到一种推导球体积公式V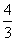＝πR³和面积公式S＝4πR²的方法，即“分割求近似值，再由近似和转化为球的体积和面积”的方法，体现了极限思想。

1．　 知识与技能

⑴通过对球的体积和面积公式的推导，了解推导过程中所用的基本数学思想方法：“分

割--求和--化为准确和”，有利于同学们进一步学习微积分和近代数学知识。

⑵能运用球的面积和体积公式灵活解决实际问题。

⑶培养学生的空间思维能力和空间想象能力。