2．注意与诱导公式，三角函数线的知识的联系

1．正弦、余弦曲线　 几何画法和五点法　

3、讲解范例：

例1 作下列函数的简图

(1)y=1+sinx，x∈[0，2π]，　 　(2) y=|sinx|，　 (3)y=sin|x|　

例2 用五点法作函数的简图.

例3　分别利用函数的图象和三角函数线两种方法，求满足下列条件的x的集合：

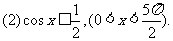
2．用五点法作正弦函数和余弦函数的简图(描点法)：

正弦函数y=sinx，x∈[0，2π]的图象中，五个关键点是：

(0,0)　 (,1)　 (p,0)　 (,-1)　 (2p,0)

余弦函数y=cosx　 xÎ[0,2p]的五个点关键是

(0,1)　 (,0)　 (p,-1)　 (,0)　 (2p,1)

只要这五个点描出后，图象的形状就基本确定了．因此在精确度不太高时，常采用五点法作正弦函数和余弦函数的简图，要求熟练掌握．

优点是方便，缺点是精确度不高，熟练后尚可以

1、用单位圆中的正弦线、余弦线作正弦函数、余弦函数的图象(几何法)：为了作三角函数的图象，三角函数的自变量要用弧度制来度量，使自变量与函数值都为实数．在一般情况下，两个坐标轴上所取的单位长度应该相同，否则所作曲线的形状各不相同，从而影响初学者对曲线形状的正确认识．

(1)函数y=sinx的图象

第一步：在直角坐标系的x轴上任取一点，以为圆心作单位圆，从这个圆与x轴的交点A起把圆分成n(这里n=12)等份.把x轴上从0到2π这一段分成n(这里n=12)等份.(预备：取自变量x值-弧度制下角与实数的对应).

第二步：在单位圆中画出对应于角，，,…，2π的正弦线正弦线(等价于“列表” ).把角x的正弦线向右平行移动，使得正弦线的起点与x轴上相应的点x重合，则正弦线的终点就是正弦函数图象上的点(等价于“描点” ).

第三步：连线.用光滑曲线把这些正弦线的终点连结起来，就得到正弦函数y=sinx，x∈[0，2π]的图象．

根据终边相同的同名三角函数值相等，把上述图象沿着x轴向右和向左连续地平行移动，每次移动的距离为2π，就得到y=sinx，x∈R的图象.

　　 把角x的正弦线平行移动，使得正弦线的起点与x轴上相应的点x重合，则正弦线的终点的轨迹就是正弦函数y=sinx的图象.

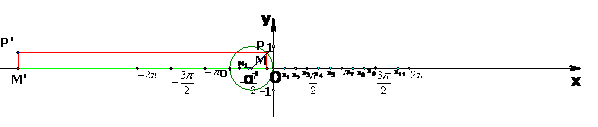
(2)余弦函数y=cosx的图象

用几何法作余弦函数的图象，可以用“反射法”将角x的余弦线“竖立”[把坐标轴向下平移，过作与x轴的正半轴成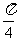角的直线，又过余弦线A的终点A作x轴的垂线，它与前面所作的直线交于A′，那么A与AA′长度相等且方向同时为正，我们就把余弦线A“竖立”起来成为AA′，用同样的方法，将其它的余弦线也都“竖立”起来．再将它们平移，使起点与x轴上相应的点x重合，则终点就是余弦函数图象上的点．]

也可以用“旋转法”把角 的余弦线“竖立”(把角x 的余弦线O₁M按逆时针方向旋转到O₁M₁位置，则O₁M₁与O₁M长度相等，方向相同.)根据诱导公式,还可以把正弦函数x=sinx的图象向左平移单位即得余弦函数y=cosx的图象. (课件第三页“平移曲线” )

正弦函数y=sinx的图象和余弦函数y=cosx的图象分别叫做正弦曲线和余弦曲线．

3.正弦线、余弦线：设任意角α的终边与单位圆相交于点P(x，y)，过P作x轴的垂线，垂足为M，则有

，

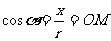
向线段MP叫做角α的正弦线，有向线段OM叫做角α的余弦线．

2.正、余弦函数定义：设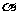是一个任意角，在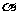的终边上任取(异于原点的)一点P(x,y)

P与原点的距离r()

则比值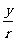叫做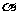的正弦　　 记作：　

　　 比值叫做的余弦　　 记作：　

1． 弧度定义：长度等于半径长的弧所对的圆心角称为1弧度的角。

(六) 评价设计

　 　作业　 P₃₀　 练习1、3　 ，B(1)

(五) 课堂小结

　　 本节课主要学习了球的体积和球的表面积公式的推导，以及利用公式解决相关的球的问题，了解了推导中的“分割、求近似和，再由近似和转化为准确和”的解题方法。