
3.有关对称轴
观察正、余弦函数的图形,可知
y=sinx的对称轴为x=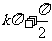 k∈Z
k∈Z
y=cosx的对称轴为x=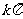 k∈Z
(1)写出函数
k∈Z
(1)写出函数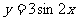 的对称轴;
(2)
的对称轴;
(2)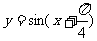 的一条对称轴是( C )
的一条对称轴是( C )
(A)
x轴, (B)
y轴,
(C) 直线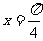 , (D) 直线
, (D) 直线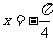
2.单调性
从y=sinx,x∈[-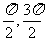 ]的图象上可看出:
]的图象上可看出:
当x∈[-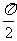 ,
,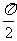 ]时,曲线逐渐上升,sinx的值由-1增大到1.
]时,曲线逐渐上升,sinx的值由-1增大到1.
当x∈[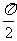 ,
,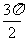 ]时,曲线逐渐下降,sinx的值由1减小到-1.
]时,曲线逐渐下降,sinx的值由1减小到-1.
结合上述周期性可知:
正弦函数在每一个闭区间[-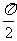 +2kπ,
+2kπ,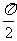 +2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[
+2kπ](k∈Z)上都是增函数,其值从-1增大到1;在每一个闭区间[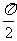 +2kπ,
+2kπ,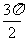 +2kπ](k∈Z)上都是减函数,其值从1减小到-1.
+2kπ](k∈Z)上都是减函数,其值从1减小到-1.
余弦函数在每一个闭区间[(2k-1)π,2kπ](k∈Z)上都是增函数,其值从-1增加到1;在每一个闭区间[2kπ,(2k+1)π](k∈Z)上都是减函数,其值从1减小到-1.
1. 奇偶性
请同学们观察正、余弦函数的图形,说出函数图象有怎样的对称性?其特点是什么?
(1)余弦函数的图形
当自变量取一对相反数时,函数y取同一值。
例如:
f(-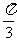 )=
)=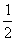 ,f(
,f(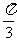 )=
)=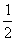 ,即f(-
,即f(-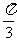 )=f(
)=f(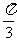 );……
);……
由于cos(-x)=cosx ∴f(-x)= f(x).
以上情况反映在图象上就是:如果点(x,y)是函数y=cosx的图象上的任一点,那么,与它关于y轴的对称点(-x,y)也在函数y=cosx的图象上,这时,我们说函数y=cosx是偶函数。
定义:一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)= f(x),那么函数f(x)就叫做偶函数。
例如:函数f(x)=x2+1, f(x)=x4-2等都是偶函数。
(2)正弦函数的图形
观察函数y=sinx的图象,当自变量取一对相反数时,它们对应的函数值有什么关系?
这个事实反映在图象上,说明函数的图象有怎样的对称性呢?函数的图象关于原点对称。
也就是说,如果点(x,y)是函数y=sinx的图象上任一点,那么与它关于原点对称的点(-x,-y)也在函数y=sinx的图象上,这时,我们说函数y=sinx是奇函数。
定义:一般地,如果对于函数f(x)的定义域内任意一个x,都有 f(-x)=-f(x) ,那么函数f(x)就叫做奇函数。
例如:函数y=x, y=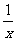 都是奇函数。
都是奇函数。
如果函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性。
注意:从函数奇偶性的定义可以看出,具有奇偶性的函数:
(1)其定义域关于原点对称;
(2)f(-x)= f(x)或f(-x)=- f(x)必有一成立。因此,判断某一函数的奇偶性时。
首先看其定义域是否关于原点对称,若对称,再计算f(-x),看是等于f(x)还是等于- f(x),然后下结论;若定义域关于原点不对称,则函数没有奇偶性。
P53:A组1 P54:B组1
2、图形变换
平移、翻转等
1、五点(画图)法
(1)作法 先作出五个关键点,再用平滑的曲线将它们顺次连结起来。
(2)用途 只有在精确度要求不高时,才能使用“五点法”作图。
(3)关键点
横坐标:0 π/2 π 3π/2 2π
●探究1
如何利用y=sinx,x∈(0,2π)的图象,通过图形变换(平移、翻转等)来得到(1)y=1+sinx ,x∈(0,2π)的图象;(2)y=sin(x- π/3)的图象?
小结:函数值加减,图像上下移动;自变量加减,图像左右移动。
●探究2
如何利用y=cos x,x∈(0,2π)的图象,通过图形变换(平移、翻转等)来得到y=-cosx ,x∈(0,2π)的图象?
小结:这两个图像关于X轴对称。
●探究3
如何利用y=cos x,x∈(0,2π)的图象,通过图形变换(平移、翻转等)来得到y=2-cosx ,x∈(0,2π)的图象?
小结:先作 y=cos x图象关于x轴对称的图形,得到 y=-cosx的图象,
再将y=-cosx的图象向上平移2个单位,得到 y=2-cosx 的图象。
●探究4
不用作图,你能判断函数y=sin( x - 3π/2 )和y=cosx的图象有何关系吗?请在同一坐标系中画出它们的简图,以验证你的猜想。
小结:sin( x - 3π/2 )= sin[( x - 3π/2 ) +2 π] =sin(x+π/2)=cosx
这两个函数相等,图象重合。
例1. 画出下列函数的简图:
(1) y=1+sinx ,x∈(0,2π)
(2) y=-cosx ,x∈(0,2π)
解:(1) 按五个关键点列表:
|
x |
0 |
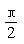 |
π |
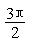 |
2π |
|
Sinx |
0 |
1 |
0 |
-1 |
0 |
|
1+ Sinx |
1 |
2 |
1 |
0 |
1 |
描点、连线,画出简图。
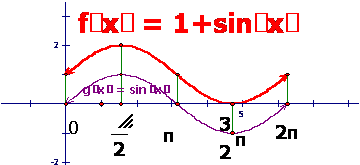
(2)按五个关键点列表:
|
x |
0 |
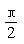 |
π |
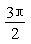 |
2π |
|
Cosx |
1 |
0 |
-1 |
0 |
1 |
|
- Cosx |
-1 |
0 |
1 |
0 |
-1 |
描点、连线,画出简图。
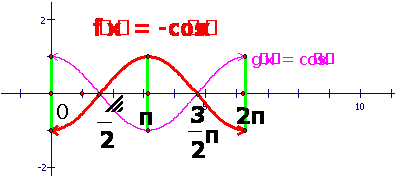
3.用五点法作出y=cosx,xÎ[0,2p]的图象
补充:1.分别用单位圆中的三角函数线和五点法作出y=sinx的图象
2.分别在[-4p,4p]内作出y=sinx和y=cosx的图象
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com