
2、说明:1°周期函数xÎ定义域M,则必有x+TÎM, 且若T>0则定义域无上界;T<0则定义域无下界;
2°“每一个值”只要有一个反例,则f (x)就不为周期函数(如f (x0+t)¹f (x0))
3°T往往是多值的(如y=sinx 2p,4p,…,-2p,-4p,…都是周期)周期T中最小的正数叫做f (x)的最小正周期(有些周期函数没有最小正周期)
y=sinx, y=cosx的最小正周期为2p (一般称为周期)
从图象上可以看出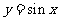 ,
, ;
;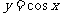 ,
, 的最小正周期为
的最小正周期为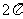 ;
;
判断:是不是所有的周期函数都有最小正周期? ( 没有最小正周期)
没有最小正周期)
1.周期函数定义:对于函数f (x),如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有:f (x+T)=f (x)那么函数f (x)就叫做周期函数,非零常数T叫做这个函数的周期。
问题:(1)对于函数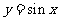 ,
, 有
有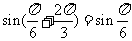 ,能否说
,能否说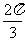 是它的周期?
是它的周期?
(2)正弦函数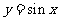 ,
, 是不是周期函数,如果是,周期是多少?(
是不是周期函数,如果是,周期是多少?(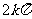 ,
,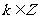 且
且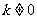 )
)
(3)若函数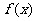 的周期为
的周期为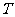 ,则
,则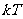 ,
,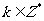 也是
也是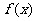 的周期吗?为什么?
的周期吗?为什么?
(是,其原因为: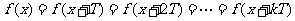 )
)
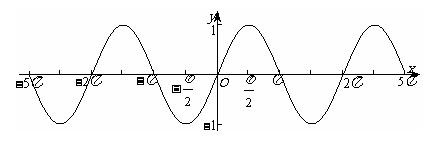
2.观察正(余)弦函数的图象总结规律:
自变量 |
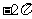 |
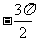 |
 |
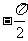 |
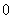 |
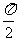 |
 |
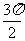 |
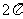 |
 函数值 函数值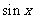 |
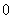 |
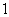 |
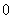 |
 |
 |
 |
 |
 |
 |
正弦函数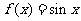 性质如下:
性质如下:
(观察图象) 1°正弦函数的图象是有规律不断重复出现的;
2°规律是:每隔2p重复出现一次(或者说每隔2kp,kÎZ重复出现)
3°这个规律由诱导公式sin(2kp+x)=sinx可以说明
结论:象这样一种函数叫做周期函数。
文字语言:正弦函数值按照一定的规律不断重复地取得;
符号语言:当 增加
增加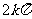 (
(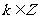 )时,总有
)时,总有 .
.
也即:(1)当自变量 增加
增加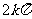 时,正弦函数的值又重复出现;
时,正弦函数的值又重复出现;
(2)对于定义域内的任意 ,
,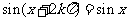 恒成立。
恒成立。
余弦函数也具有同样的性质,这种性质我们就称之为周期性。
1.问题:(1)今天是星期二,则过了七天是星期几?过了十四天呢?……
(2)物理中的单摆振动、圆周运动,质点运动的规律如何呢?
3.
2.
1.
练习讲评
(1)化简: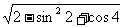 (2)已知非零常数
(2)已知非零常数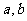 满足
满足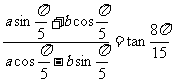 ,求
,求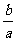 的值;
(3)已知
的值;
(3)已知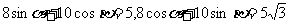 求值:(1)
求值:(1) ;(2)
;(2)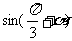 解:
(1)
解:
(1)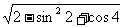
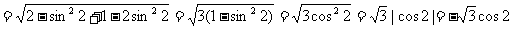 (2)
(2)
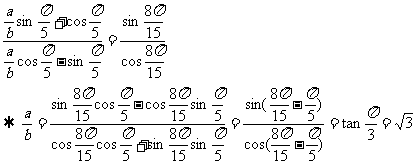 (3)两式平方相加得
(3)两式平方相加得
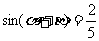 ;
;
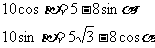 两式平方相加得
两式平方相加得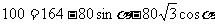 即
即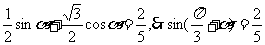
1.
有关奇偶性
(1)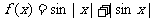 (2)
(2)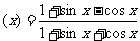
有关单调性
(1)利用公式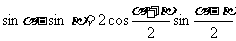 ,求证
,求证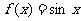 在
在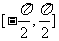 上是增函数;
(2)不通过求值,指出下列各式大于0还是小于0;
①
上是增函数;
(2)不通过求值,指出下列各式大于0还是小于0;
①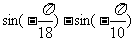 ;
②
;
②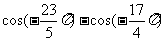 (3)比较
(3)比较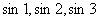 大小;
大小;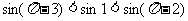 (4)求函数
(4)求函数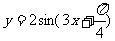 的单调递增区间;
的单调递增区间;
4.例题讲解
例1 判断下列函数的奇偶性
(1)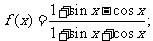
(2)f(x)=sin4x-cos4x+cos2x;
(3)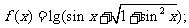
(4)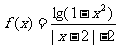
(5)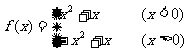 ;
;
例2 (1)函数f(x)=sinx图象的对称轴是 ;对称中心是 .
(2)函数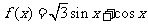 图象的对称轴是 ;对称中心是
.
图象的对称轴是 ;对称中心是
.
例3 已知f(x)=ax+bsin3x+1(a、b为常数),且f(5)=7,求f(-5).
例4 已知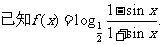
(1) 求f(x)的定义域和值域;
(2) 判断它的奇偶性、周期性;
(3) 判断f(x)的单调性.
例5 (1)θ是三角形的一个内角,且关于x 的函数f(x)=sain(x+θ)+cos(x-θ)是偶函数,求θ的值.
(2)若函数f(x)=sin2x+bcos2x的图象关于直线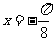 对称,求b的值.
对称,求b的值.
例6 已知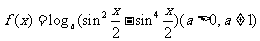 ,试确定函数的奇偶性、单调性.
,试确定函数的奇偶性、单调性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com