
1.因为正切函数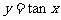 的定义域是
的定义域是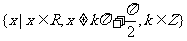 ,所以它的图象被
,所以它的图象被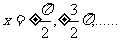 等相互平行的直线所隔开,而在相邻平行线间的图象是连续的。
等相互平行的直线所隔开,而在相邻平行线间的图象是连续的。
P.71.练习2,3,6
求函数y=tan2x的定义域、值域和周期、并作出它在区间[-π,π]内的图象
解:(1)要使函数y=tan2x有意义,必须且只须2x≠ +kπ,k∈Z
+kπ,k∈Z
即x≠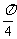 +
+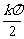 ,k∈Z
,k∈Z
∴函数y=tan2x的定义域为{x∈R|,x≠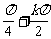 ,k∈Z}
,k∈Z}
 (2)设t=2x,由x≠
(2)设t=2x,由x≠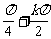 ,k∈Z}知t≠
,k∈Z}知t≠ +kπ,k∈Z
+kπ,k∈Z
∴y=tant的值域为(-∞,+∞)
即y=tan2x的值域为(-∞,+∞)
(3)由tan2(x+ )=tan(2x+π)=tan2x
)=tan(2x+π)=tan2x
∴y=tan2x的周期为 .
.
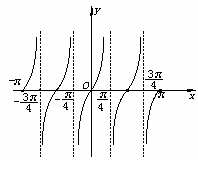
(4)函数y=tan2x在区间[-π,π]的图象如图
6.讲解范例:
例1比较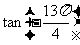 与
与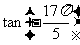 的大小
的大小
解: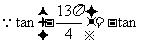
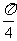 ,
,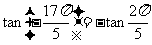 ,
,
又: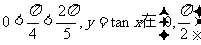 内单调递增,
内单调递增,
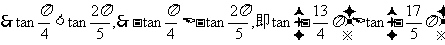

例2讨论函数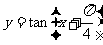 的性质
的性质
略解:定义域: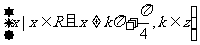
值域:R 奇偶性:非奇非偶函数
单调性:在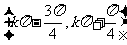 上是增函数
上是增函数
图象:可看作是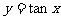 的图象向左平移
的图象向左平移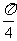 单位
单位
例3求函数y=tan2x的定义域
解:由2x≠kπ+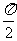 ,(k∈Z)
,(k∈Z)
得x≠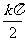 +
+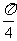 ,(k∈Z)
,(k∈Z)
∴y=tan2x的定义域为:{x|x∈R且x≠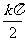 +
+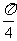 ,k∈Z}
,k∈Z}
例4观察正切曲线写出满足下列条件的x的值的范围:tanx>0
解:画出y=tanx在(-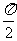 ,
,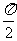 )上的图象,不难看出在此区间上满足tanx>0的x的范围为:0<x<
)上的图象,不难看出在此区间上满足tanx>0的x的范围为:0<x<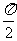
结合周期性,可知在x∈R,且x≠kπ+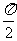 上满足的x的取值范围为(kπ,kπ+
上满足的x的取值范围为(kπ,kπ+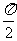 )(k∈Z)
)(k∈Z)
例5不通过求值,比较tan135°与tan138°的大小
解:∵90°<135°<138°<270°
又∵y=tanx在x∈(90°,270°)上是增函数
∴tan135°<tan138°
5.余切函数y=cotx的图象及其性质(要求学生了解):
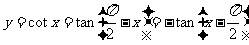 --即将
--即将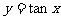 的图象,向左平移
的图象,向左平移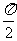 个单位,再以x轴为对称轴上下翻折,即得
个单位,再以x轴为对称轴上下翻折,即得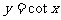 的图象
的图象
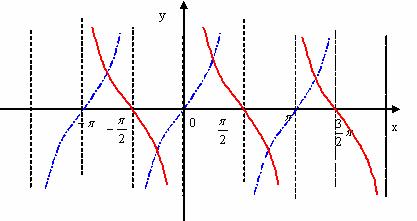
定义域: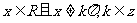
值域:R,
当 时
时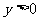 ,当
,当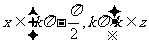 时
时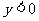
周期:
奇偶性:奇函数
单调性:在区间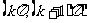 上函数单调递减
上函数单调递减
4.正切函数的性质 引导学生观察,共同获得:
(1)定义域: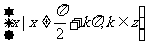 ;
;
(2)值域:R
观察:当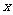 从小于
从小于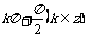 ,
,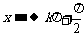 时,
时,
当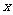 从大于
从大于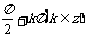 ,
,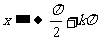 时,
时, 。
。
(3)周期性: ;
;
(4)奇偶性:由 知,正切函数是奇函数;
知,正切函数是奇函数;
(5)单调性:在开区间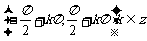 内,函数单调递增。
内,函数单调递增。
3.作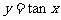 ,
,
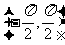 的图象
的图象
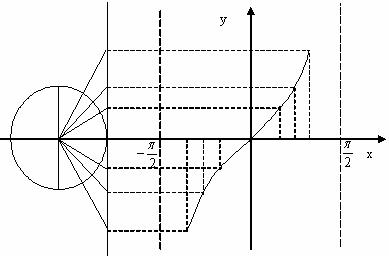
说明:(1)正切函数的最小正周期不能比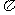 小,正切函数的最小正周期是
小,正切函数的最小正周期是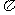 ;
;
(2)根据正切函数的周期性,把上述图象向左、右扩展,得到正切函数
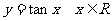 ,且
,且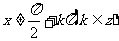 的图象,称“正切曲线”。
的图象,称“正切曲线”。

(3)由图象可以看出,正切曲线是由被相互平行的直线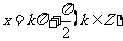 所隔开的无穷多支曲线组成的。
所隔开的无穷多支曲线组成的。
2.正切函数是不是周期函数?
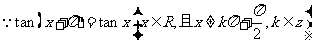 ,
,
∴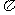 是
是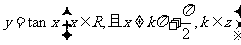 的一个周期。
的一个周期。
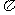 是不是正切函数的最小正周期?下面作出正切函数图象来判断。
是不是正切函数的最小正周期?下面作出正切函数图象来判断。
1.正切函数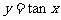 的定义域是什么?
的定义域是什么?
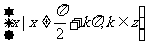
问题:正弦曲线是怎样画的?
正切线?
练习正切线,画出下列各角的正切线:
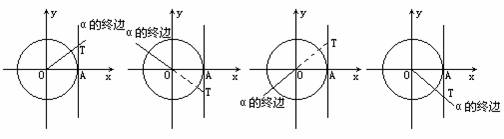 .
.
下面我们来作正切函数和余切函数的图象.
题选
求下列函数的周期:
(1)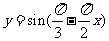 ; (2)
; (2)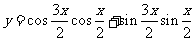 ;
;
(3)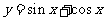 ; (4)
; (4) ; (5)
; (5)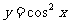 .
.
解:(1)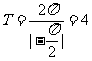 ,∴周期为
,∴周期为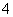 ;
;
(2)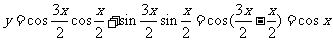 ,∴周期为
,∴周期为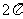 ;
;
(3)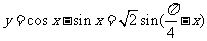 ∴周期为
∴周期为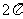 ;
;
(4) ,∴周期为
,∴周期为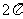 ;
;
(5)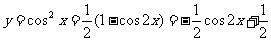 ,∴周期为
,∴周期为 .
.
说明:求函数周期的一般方法是:先将函数转化为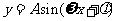 的形式,再利用公式
的形式,再利用公式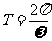 进行求解。
进行求解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com