
正切函数的性质。
5.函数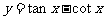 的奇偶性是 奇函数 ,周期是
的奇偶性是 奇函数 ,周期是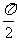 .
.
4.函数 的值域是
的值域是 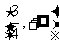 .
.
3.函数 的定义域是
的定义域是 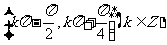 .
.
2.与函数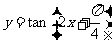 的图象不相交的一条直线是( D
)
的图象不相交的一条直线是( D
)
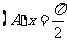
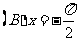
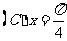
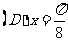
1.“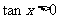 ”是“
”是“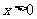 ”的 既不充分也不必要 条件。
”的 既不充分也不必要 条件。
例1:求下列函数的周期:
(1)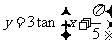 答:
答: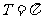 。
。
(2)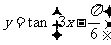 答:
答: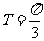 。
。
说明:函数 的周期
的周期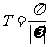 .
.
例2:求函数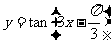 的定义域、值域,指出它的周期性、奇偶性、单调性,并说明它的图象可以由正切曲线如何变换得到。
的定义域、值域,指出它的周期性、奇偶性、单调性,并说明它的图象可以由正切曲线如何变换得到。
解:由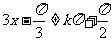 得
得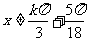 ,
,
∴所求定义域为 ,值域为R,周期
,值域为R,周期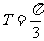 ,是非奇非偶函数,在区间
,是非奇非偶函数,在区间 上是增函数。
上是增函数。
将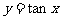 图象向右平移
图象向右平移 个单位,得到
个单位,得到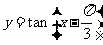 的图象;再将
的图象;再将
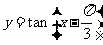 的图象上所有点的横坐标变为原来的
的图象上所有点的横坐标变为原来的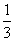 倍(纵坐标不变),就得到函数
倍(纵坐标不变),就得到函数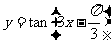 的图象。
的图象。
例3:用图象求函数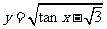 的定义域。
的定义域。
解:由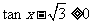 得
得 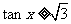 ,
,
利用图象知,所求定义域为 ,
,
 亦可利用单位圆求解。
亦可利用单位圆求解。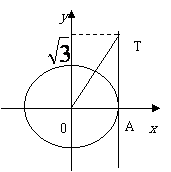
2.回忆正切函数的性质:定义域、值域、周期性、奇偶性、单调性。
1.作正切曲线的简图,说明正切曲线的特征。
2.作出正切函数的图象,也是先作出长度为一个周期(-π/2,π/2)的区间内的函数的图象,然后再将它沿x轴向左或向右移动,每次移动的距离是π个单位,就可以得到整个正切函数的图象。
讨论函数的单调性应借助图象或相关的函数的单调性;形如y=tan(ωx),x≠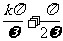 (k∈Z)的周期T=
(k∈Z)的周期T= ;注意正切函数的图象是由不连续的无数条曲线组成的
;注意正切函数的图象是由不连续的无数条曲线组成的
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com